Page 136 - 《爆炸与冲击》2025年第5期

第 45 卷 钱秉文，等： 超高速撞击条件下混凝土靶体内 应力波的测量和分析 第 5 期

压电应力计记录靶体在弹道轴线上 3 个不同位 90 Transmission wave

置处（分别距撞击面 70、100 和 130 mm，对应传 strain signal
PVDF test signal
感器 P1、P2 和 P3，如图 4 所示）的应力波形，如 60
图 11(a) 所示。可以看出，波形的信噪比较高，能
区分波形的起跳点、上升沿、峰值、下降沿等， Equivalent charge/nC
说明应力计的选取、标定、埋设和保护工艺能满 30
足超高速撞击条件下混凝土靶中应力波的测量
需求。 0
0 0.1 0.2
由图 11(a) 可知，应力波抵达后先迅速升高 t/ms
至峰值，随后又出现了 1 个次级峰值，并持续一
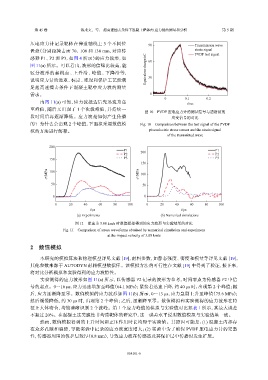
图 10 PVDF 压电应力计的测试信号与透射波的
段时间后再逐渐降低。应力波是如何产生传播 应变信号的对比
的？为什么会出现 2 个峰值，下面拟采用数值模 Fig. 10 Comparison between the test signal of the PVDF
拟的方法进行解释。 piezoelectric stress sensor and the strain signal

of the transmitted wave
200

P1 200 P1
P2 P2
150 P3 P3
150
σ/MPa 100 σ/MPa 100

50 50

0 0
0 20 40 60 80 100 0 20 40 60 80 100
t/μs t/μs
(a) Experiments (b) Numerical simulations
图 11 弹速为 3.08 km/s 时数值模拟得到的应力波形与实验结果的对比
Fig. 11 Comparison of stress waveforms obtained by numerical simulation and experiment
at the impact velocity of 3.08 km/s

2 数值模拟

本研究的模拟算法和物理模型详见文献 [19]，材料参数，如静态强度、密度和模量等详见文献 [19]，
其他参数来源于 AUTODYN 材料模型数据库。该模拟方法的可行性在文献 [19] 中得到了验证，接下来，
将对比分析模拟和实验得到的应力波特性。
实验测得的应力波形如图 11(a) 所示，以传感器 P2 记录的波形为参考，时间零点为传感器 P2 中信
号的起点。0～16 μs，应力迅速增加至峰值（64.1 MPa）；紧接着迅速下降，约 40 μs 时，出现第 2 个峰值；随
后，应力逐渐降至零。数值模拟的应力波形如图 11(b) 所示，0～13 μs，应力急剧上升至峰值（75.6 MPa）；
然后缓慢降低，约 30 μs 时，出现第 2 个峰值；之后，逐渐降至零。数值模拟和实验测得的应力波形在特
征上大体吻合，均能清晰识别 2 个波峰。第 1 个应力峰值的模拟与实验值对比如表 1 所示，其最大误差
不超过 20%。在混凝土这类脆性非均质靶体的研究中，这一误差水平说明数值模拟与实验结果一致。
然而，数值模拟得到的上升时间和正压作用时长均短于实验值。其原因可能是：(1) 混凝土内部存
在众多孔隙和裂缝，导致实验中记录的应力波宽度增大；(2) 实验中为了确保 PVDF 压电应力计的完整
性，传感器周围的保护层较厚（0.8 mm），导致应力波在传感器及其保护层中传播时发生扩展。

054101-6