Page 80 - 《爆炸与冲击》2023年第2期

第 43 卷 刘 伟，等： 波形控制器对杀伤战斗部破片飞散特性影响研究 第 2 期

b−1
ρ m0 a sinφ 0
= + (13)
ρ m b b Dsinφ 3
Å ã
ρ m0
1− tanφ 3
ρ m
tanε = (14)
ρ m0 2
1+ tan φ 3
ρ m
ρ m0 为波形控制器材料初始密度，q 为（Ⅲ）区气体流动速度，ρ 为（Ⅲ）区密度，p 为（Ⅲ）区气体压
m
m
m
式中：
a b 为与材料性质有关的常数，可根据试验得到，其 Hugoniot 关系为：
力， φ 3 为透射冲击波与界面夹角， 、
(15)
D m = a+bu m
最后根据界面处的压力连续条件可得：
(16)
p 2 = p m
φ 3 和冲击波在波
联立式（11）～（16）可求解出爆轰波在波形控制器中透射的斜冲击波与界面的夹角
形控制器中的传播速度。然后结合 Shapiro 公
v 0
式 ， 由 数 值 拟 合 的 方 法 得 到 波 形 控 制 器 曲 线 。
θ s
Shapiro 公式为：
( ) D e
v 0 π
tanθ s = cos −θ 1 +θ 2 (17)
2D e 2
θ 1 为壳体法线方向与战斗部中心轴线的夹角，
式中：
θ s 为
θ 2 为爆轰波阵面法线方向与中心轴线的夹角，
破片速度矢量偏离壳体法线的夹角，如图 3 所示。
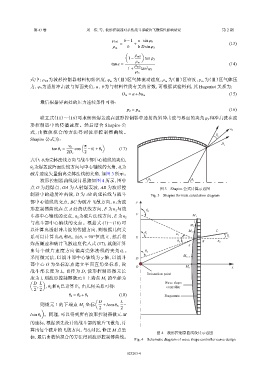
波形控制器曲线设计思路如图 4 所示，图中 θ 2 θ 1

点 O 为起爆点，OA 为入射爆轰波，AB 为波形控 图 3 Shapiro 公式计算示意图
制器中的透射冲击波，D 为 AB 的延长线与战斗 Fig. 3 Shapiro formula calculation diagram
部中心轴线的交点，BC 为破片飞散方向， n 1 为波 y
形控制器曲线在点 A 处的法线方向，F n 1 与战
为
θ 4
F
n 2 为破片法线方向，E M 1
斗部中心轴线的交点， 为 n 2
与战斗部中心轴线的交点。根据式 (1)～(16) 可 l
M 2
以计算出透射冲击波的传播方向，则根据几何关 C
θ 1 n 1 M 3
θ 1 = 90°恒成立，然后将 E θ s
系可以计算出 θ 2 和 θ 3 ，而
炸药爆速和破片飞散速度代入式 (17)，就能计算 θ 3 A B n 2
出 每 个 破 片 速 度 方 向 偏 离 壳 体 法 线 的 夹 角 θ s 。 θ 2
采用微元法，以战斗部中心轴线为 y 轴，以战斗 D M n−1
部中心 O 为坐标原点建立平面直角坐标系，设
O M n x
战斗部长度为 L，直径为 D，波形控制器微元长
Detonation point
度为 l，则波形控制器微元 1 上端点 M 的坐标为
1
Å ã Wave shape
D L
, ， θ 2 和 θ 3 已计算出，由几何关系可得: controller
2 2
(18)
θ 4 = θ 2 +θ 3 Fragments
Å
D L
则微元 1 的下端点 M 坐标 +lcosθ 4 , −
1
2 2
ã
。同理，可以得到所有波形控制器微元
lsinθ 4 M
的坐标，根据预先设计的战斗部的破片飞散角，计
θ s 对比，修正 M 点坐
算出每个破片的飞散方向，与
图 4 波形控制器曲线设计示意图
标，最后由数值拟合的方法得到波形控制器曲线。
Fig. 4 Schematic diagram of wave shape controller curve design
023203-4