Page 194 - 《软件学报》2020年第12期

3860 Journal of Software 软件学报 Vol.31, No.12, December 2020

上的仿真评估了本文所提算法的性能.
5.1 基准算法
• 穷举法
通过穷举的方式遍历所有可能的节点部署及调度方案,从中选出全局最优解,其时间复杂度较高.给定 K 个
()i
K
节点,节点部署位置的排列组合有 C 种,每个节点调度方案至多有 C B J max 种.因此,穷举法的时间复杂度为
I
( ∑
() i
OJN I C K 1∏ () h C B max ) .
h= i s ∈ S J
(h)
其中,S ⊆S 表示节点部署位置的第 h 个排列组合,只能用于小规模网络.
• 分阶段贪婪算法
简写为 TSGA(two-stage greedy algorithm) [27] ,将传感节点的部署与调度分开考虑,分为两个阶段.
(1) 第 1 阶段,假定每个传感节点在所有时隙均处于工作模式,TSGA 迭代地遍历所有未部署节点的候选
部署位置,每次选择使得检测质量最大的位置放置节点.该阶段的时间复杂度为 O(KIN);
(2) 第 2 阶段,依次确定这 K 个节点的调度方案,TSGA 遍历所有部署节点的所有时隙,每次选择使得检测
质量 Q 值最大的时隙作为节点的工作时隙.该阶段的时间复杂度为 O(KJ(N+logJ)).
综上所述,分阶段贪婪算法的时间复杂度为 O(K(IN+JN+JlogJ))).我们将分别在小规模和大规模网络中以
及利用真实数据集将提出的 JOGA 与 TSGA 进行性能比较.
5.2 参数设置

小规模网络的区域大小为 3m×3m.监测点随机分布在区域内,1 个能量源和 5 个传感节点候选部署位置规
则分布,如图 2(a)所示.进一步设定 P s =3W,K=3,J=4,W 0 =10W.融合半径 R 的取值根据第 4.1 节的分析得到,R=
1.97m.
大规模网络的区域大小为 30m×30m.监测点同样随机分布在区域内,9 个能量源和 121 个候选部署位置规
则分布,如图 2(b)所示.且设定 J=8,W 0 =72W.融合半径 R 的取值同样基于第 4.1 节的分析得到,R=5.28m.

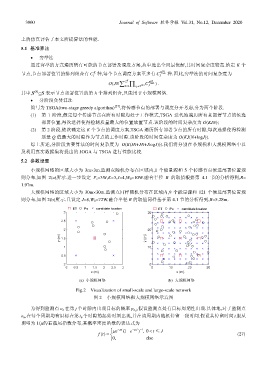
(a) 小规模网络 (b) 大规模网络

Fig.2 Visualization of small-scale and large-scale network
图 2 小规模网络和大规模网络示意图
为得到监测点 o n 在第 j 个时隙内出现目标的概率 p n,j ,假设监测点处有目标周期性出现.具体地,对于监测点
o n ,在每个周期均有目标在第 t n 个时隙的起始时刻出现,并在该周期内随机停留一段时间.假设其停留时间 t 服从
期望为 1/μ的右截尾指数分布,其概率密度函数的表达式为
−
<
1
⎧ ⎪ μ e − t μ (1 e − μ J − ) , 0 t ≤ J
ft (27)
() = ⎨
⎪ ⎩ 0, else