Page 192 - 《软件学报》2020年第12期

3858 Journal of Software 软件学报 Vol.31, No.12, December 2020

4.1 融合半径分析
融合半径的设定,对最终的检测性能有关键影响:如果设定的融合半径过大,较远节点低信噪比的采样结果
参与融合会导致检测性能下降.我们举例说明该问题:假设节点 s 1 和 s 2 分别距离目标 d 1 和 d 2 ,令 d 1 =10m,将 d 2
从 10m 变化至 20m,并且将融合半径设置为与 d 2 相等的值,比较由单个节点 s 1 得出的检测率 P D (s 1 )和由节点 s 1 ,s 2
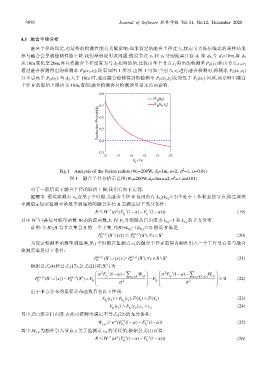
通过融合检测得出的检测率 P D (s 1 ,s 2 ),结果如图 1 所示.由图 1 可知:当引入 s 2 进行融合检测时,检测率 P D (s 1 ,s 2 )
并不总高于 P D (s 1 ).当 d 2 大于 16m 时,通过融合检测得到的检测率 P D (s 1 ,s 2 )反而低于 P D (s 1 ).因此,该示例中融合
半径 R 的取值上限应为 16m,否则,融合检测会对检测质量带来负面影响.

2
Fig.1 Analysis of the fusion radius (W 0 =200W, d 0 =1m, u=2, σ =1, α=0.01)
2
图 1 融合半径分析示意图(W 0 =200W,d 0 =1m,u=2,σ =1,α=0.01)
对于一般情况下融合半径的取值上限,我们有如下定理:
定理 2. 假设监测点 o n 在第 j 个时隙,其融合半径 R 范围内有 k n,j (k n,j ≥2)个处于工作状态的节点,给定虚警
率阈值α,保证检测率函数单调递增的融合半径 R 需满足以下充分条件:
R W − 1 (σ ≤ 2 (F − 2 Y 1 (1 α − ) F− − 1 Y 1 (1 α − ))) (19)
−1
其中 W (⋅)是信号能量函数 W(d)的逆函数,Y 1 和 Y 2 分别服从自由度为 k n,j −1 和 k n,j 的卡方分布.
证明:令 S′⊆S 为节点集合 S 的一个子集,且|S′|=k n,j −1(k n,j ≥2).假设 S′满足:
P D (,)nj ( ′ \{ })s ≤ P D ( ,)nj ( ), s∀∈S ′ S S ′ (20)
为保证检测率函数单调递增,第 j 个时隙在监测点 o n 的融合半径 R 范围内额外引入一个工作节点参与融合
检测需满足以下条件:
\ ′ ∀
P D (, )nj ( ′ ∪ S { })s ≥ P D ( , )nj ( ), s∈ S ′ S S (21)
根据公式(4)和公式(17),公式(21)可改写为
⎛ σ 2 F − 1 (1 α ) − ∑ W ⎞ ⎛ − σ 2 F − 1 (1 α − ) − ∑ W ⎞
nj
nj
P D (, ) ( ′ { })s − P D ( , ) ( ) ′ ∪ S = S F ⎜ 1 Y ⎜ 1 Y 2 i s ∈ ′ , i n ⎟ ⎟ − F ⎜ 2 Y ⎜ 2 Y 2 i s ∈S S ′ ∪ {} s , i n ⎟ ⎟ ≥ 0 (22)
⎝ σ ⎠ ⎝ σ ⎠
由于卡方分布的累积分布函数具有以下性质:
() >
Fc F (), ( )c D Y < D ( )Y (23)
1 Y 1 2 Y 1 1 2
() >
Fc F ( ),c c > c (24)
1 Y 1 1 Y 2 1 2
其中,D(⋅)表示自由度.由此可推断出满足不等式(22)的充分条件:
W ≥ σ 2 (F − 2 Y 1 (1 α − ) F− − 1 Y 1 (1 α − )) (25)
, sn
其中,W s,n 为额外引入节点 s 关于监测点 o n 的采样值.根据公式(1)可得:
R W − 1 (σ ≤ 2 (F − 1 (1 α − ) F− − 1 (1 α − ))) (26)
2 Y 1 Y