Page 158 - 《软件学报》2020年第12期

3824 Journal of Software 软件学报 Vol.31, No.12, December 2020

在现实世界中,很多图数据上都带有时序信息,例如电信话务网络、金融交易网络、道路交通网络和在线
社交网络等等.而环路作为一种特殊的结构,在各种图中都频繁出现,并且拥有着重要的意义.目前,时序环已经
[1]
开始被应用于多个领域,有了多种实际应用.比如在生物领域,时序环可以表示某种生物反馈机制 ;在金融领
[2]
域,检测出的时序环可能代表了某一种金融诈骗行为 .攫取时序图结构,可以帮助我们挖掘未知的图模式.图 1
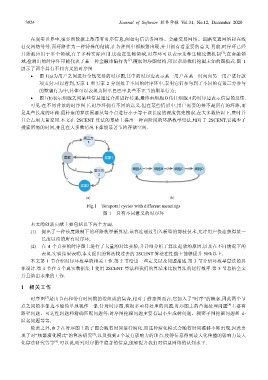
展示了两个具有不同含义的时序图.
• 图 1(a)为用户之间进行金钱交易的时序图,其中的时序边表示某一用户在某一时间向另一用户进行款
项支付.可以看到,买家 1 和买家 2 分别处于不同的时序环中,表明它们参与到了不同的有第三方参与
的欺骗行为中,具体可以表现为阿里巴巴中某些不正当的刷单行为;
• 图 1(b)表示细胞之间某些信息通过介质进行传递,最终由细胞 D 传往细胞 A 的时序边表示信息的反馈.
可见:在不同背景的时序图下,时序环拥有不同的意义.但在某些情形中,用户需要的并不是所有的环路,而
是某些长度的环路.最朴素的算法需要从每个点进行小于等于该长度的深度优先搜索,在大多数情况下,费时并
且会占用大量空间.本文在 2SCENT 算法的基础上提出一种两阶段的环路枚举算法,相对于 2SCENT,它减少了
搜索所需的时间,并且在大多数情况下都能显著节约存储空间.

Fig.1 Temporal cycles with different meanings
图 1 具有不同意义的时序环

本文的创新贡献主要包括以下两个方面.
(1) 提出了一种长度限制下的环路枚举新算法.该算法通过引入新型的剪枝技术,允许用户快速获得某一
长度以内的所有时序环;
(2) 在 4 个真实的时序图上进行了大量的对比实验,并详细分析了算法起效的原因,以及在不同情况下的
表现.实验结果表明,本文提出的算法较过去的 2SCENT 算法在性能上能够提升 50%以上.
本文第 1 节介绍时序环枚举的相关工作.第 2 节给出一些定义以及问题描述.第 3 节介绍环枚举算法的具
体设计.第 4 节在 4 个真实数据集上使用 2SCENT 算法和我们的算法来比较算法的运行效率.第 5 节总结全文
并且给出未来的工作.

1 相关工作

[3]
时序图 是由节点和带有时间戳的边组成的集合,相对于静态图而言,它加入了“时序”的概念,因此两个节
[4]
点之间的多条边不能简单地视作一条.针对时序图,有很多亟待处理的问题.时序图上的查询处理问题 主要有
路径问题、可达性问题和精确匹配问题等;时序图挖掘问题主要有最小生成树问题、稠密子图挖掘问题和 k-
匿名问题等等.
除此之外,由于在时序图上的子图会随着时间进行演化,而这种演化模式会随着时间推移不断出现,因此出
[5]
现了对“频繁演化模式”的算法研究 ,以及找到 k 个最有影响力的顶点,使得信息得到最大化传播的影响力最大
[6]
化算法研究等等 .可以说,研究时序图中隐含的信息,能够提升我们对信息网络的认知水平.