Page 29 - 《软件学报》2020年第11期

刘中舟 等:动态基因调控网演化分析 3345

分解维度为 16 为宜,过低则算法表现较差,过高则增加无意义的计算开销.
(2) MT 算法的 AUC 值随张量分解的维度增加无明显变化趋势,只是一直围绕着固定值做小于±0.1 的波
动.因此可得出,张量分解的维度仅对算法的准确率有影响,而对衡量算法表现的另一指标 AUC 无明
显影响.
3.2.2 基于隐空间特征的动态基因调控网符号判别算法
本文提出的 DGNE 方法中的基于隐空间特征的符号判别算法是以隐空间特征和显示特征共同作为符号判
别的特征向量,对基因调控网中边的符号进行学习.为探究在特征向量中两类特征的比例对算法效果的影响,即
隐空间特征向量的维度对算法的影响,需要对此算法中非负矩阵三因子的分解维度 k 进行参数检验,以确定最
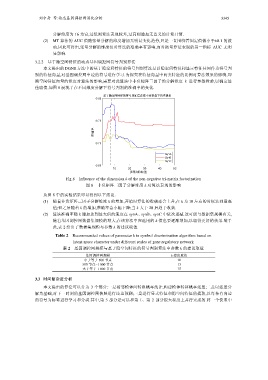
佳取值.如图 8 展现了在不同维度分解下符号判别的准确率的变化.

Fig.8 Influence of the dimension k of the non-negative tri-matrix factorization
图 8 非负矩阵三因子分解维度 k 对算法表现的影响
从图 8 中的实验结果可以得到以下结论.
(1) 随着非负矩阵三因子分解维度 k 的增加,开始时算法的准确率会上升,在 k 为 10 左右的时候达到最高
值;但之后随着 k 的增加,准确率会小幅下降;当 k 大于 20 后趋于收敛.
(2) 算法准确率随 k 增加达到最大值的速度在 synA、synB、synC 中依次递减.这可能与数据集规模有关,
随着基因调控网数据集规模的增大,在该算法中应选用的 k 值也要逐渐增加,以取得更好的效果.鉴于
此,表 2 给出了数据集规模与参数 k 的建议取值.
Table 2 Recommended values of parameter k in symbol discrimination algorithm based on
latent space character under different scales of gene regulatory network
表 2 基因调控网规模与基于隐空间特征的符号判别算法中参数 k 的建议取值
基因调控网规模 k 建议取值
小于等于 500 节点 10
500 节点~1 000 节点 13
大于等于 1 000 节点 15

3.3 时间复杂度分析
本文提出的算法可以分为 3 个部分:一是相邻模体间转换概率统计,构建模体转移概率张量;二是以张量分
解为基础,对下一时刻的基因调控网快照进行连边预测;三是进行显式特征和隐空间特征的提取,以每条有向边
的符号为标签进行学习和分类.其中,第 3 部分是可以和第 1、第 2 部分很大程度上并行完成的.将一个快照中