Page 295 - 《软件学报》2025年第12期

5676 软件学报 2025 年第 36 卷第 12 期

个子领域重要程度、每个三元组被访问的概率等信息, 定义三元组的重要性, 采用加权均值度量其准确性, 细化评
估的粒度, 此时评估结果更符合应用场景、贴近用户体验. 本文从嵌入模型表征能力、知识图谱稠密度、三元组
重要性计算方式等多个角度, 分析比较了对评估方法性能的影响. 实验表明, 相比现有知识图谱准确性的自动化评
估方法, 在零样本条件下, 本文所提出的方法可有效降低评估误差, 平均降低接近 30%, 在错误率较高、稠密图谱
的数据集上效果尤为显著.

样本评估
判断依据

样本选取 人工标注 知识图谱
知识图谱
匹配验证 匹配程度 准确性评估
外部知识库 度量
图谱内部信息

样本正确率
分类模型 三元组分类
统计

阈值 负样本 训练集

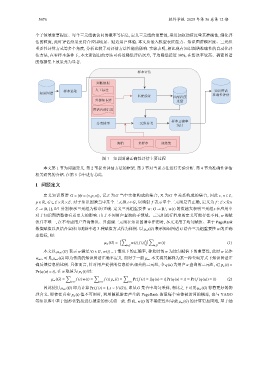
图 1 知识图谱正确性评估主要过程

本文第 1 节为问题定义. 第 2 节提出评估方法的框架. 第 3 节对当前方法进行实验分析. 第 4 节为准确性评估
相关研究的介绍. 在第 5 节中进行总结.
1 问题定义

定义知识图谱 G = {t|t = (s, p,o)}, 记 E 为 G 当中实体构成的集合, R 为 G 中关系构成的集合, 因此 s, o ∈ E,
p ∈ R, G ⊆ E ×R×E . 对于知识图谱当中某个三元组 t ∈ G, 以映射 f 表示单个三元组是否正确, 定义为 f : E ×R×
+
E → {0,1}, 0/1 分别表示三元组为错误/正确. 定义三元组重要性 w : G → R , w(t) 的值越大表明三元组 在应用中
t
对于知识图谱整体有着更大的影响. 由于不同用户查询的子领域、三元组流行程度的定义可能存在不同, w 的赋
值并不唯一, 在不考虑用户查询情况、只强调三元组在知识图谱中作用时, 本文采用了均匀赋值、基于 PageRank
数值赋值以及结合实体出现频率这 3 种赋值方式作为样例. 以 µ w (G) 表示知识图谱 G 结合三元组重要性 w 的正确
率指标, 则:

(∑ )/ ∑
µ w (G) = w(t) f (t) w(t) (1)
t∈G t∈G
本文以 µ uni (G) 表示 w 满足 ∀t ∈ G, w(t) = 1 情况下的正确率, 称此时的 w 为均匀赋值下的重要性, 此时 w 记作
w uni , 可见 µ uni (G) 即为传统的知识图谱正确率定义. 而对于一般 µ w , 本文将其解释为某一种查询方式下知识图谱正
确反馈信息的比例. 具体而言, 针对用户提供的信息给出相关的三元组, 令 q(u) 为用户 u 查询的三元组, 记 p u (t) =
Pr(q(u) = t), 在 w 取值为 p u (t) 时:

∑ ∑ ∑
( )
µ w (G) = f (t)w(t) = f (t) p u (t) = Pr f (t) = 1|q(u) = t Pr(q(u) = t) = Pr( f (q(u)) = 1) (2)
t∈G t∈G t∈G
因此使用 µ uni (G) 即为计算 Pr( f (t) = 1,t ∼ U (G)), 即从 G 集合中均匀采样, 相比之下可见 µ w (G) 有着更好的物
p u (t) 值不可用时, 利用随机游走产生的 PageRank 衡量每个实体被访问的概率, 也与 YAGO
理含义. 即使在真实
等知识库中基于图形化链接进行搜索的形式相一致. 然而, w(t) 的不确定性也导致 µ w (G) 的计算更加困难, 基于抽