Page 168 - 《软件学报》2025年第12期

欧阳继红 等: HSDiag: 变种碰集算法求解诊断 5549

26 22
MCS-MHS MCS-MHS
HSDiag 20 HSDiag
诊断解个数 (×10 5 ) 16 诊断解个数 (×10 5 ) 18
21
16
14
11
12
6 10
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
电路实例数 电路实例数
(a) c499 (b) c1355
20 25
MCS-MHS MCS-MHS
HSDiag 20 HSDiag
诊断解个数 (×10 5 ) 10 诊断解个数 (×10 5 ) 15
15

10

0
0 5 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
电路实例数 电路实例数
(c) c1908 (d) c880
MCS-MHS MCS-MHS
HSDiag 0.3 HSDiag
诊断解个数 (×10 5 ) 10 5 诊断解个数 (×10 5 ) 0.2
15

0.1

0 0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
电路实例数 电路实例数
(e) c3540 (f) c6288
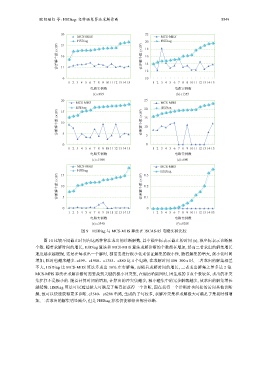
图 9 HSDiag 与 MCS-MHS 算法在 ISCAS-85 电路实验比较

图 10 比较不同截止时间内这两种算法求出的诊断解数, 其中横坐标表示截止的时间 (s), 纵坐标表示诊断解
个数. 随着求解时间的增长, HSDiag 算法和 MCS-MHS 算法求解诊断的个数都在增加, 然而二者求出的解集增长
速度越来越缓慢, 这是在每求出一个解时, 都需要进行极小化来保证解集的极小性, 随着解集的增大, 极小化时间
增加, 耗时也越来越多. c499、c1908、c1355、c880 这 4 个电路, 在求解时间 100–300 s 时, 二者求出的解集相差
不大, HSDiag 比 MCS-MHS 算法多求出 30% 左右解集, 而随着求解时间的增长, 二者求出解集之差多达 2 倍.
MCS-MHS 算法在求解诊断时需要找到关键的极小冲突集, 在遍历哈斯图时, 因生成的节点个数较多, 求出的冲突
集往往不是极小的. 随着计算时间的增加, 计算出的冲突集越多, 极小碰集中的冗余解就越多, 故求出的解集增长
越缓慢. HSDiag 算法可以通过极大可满足子集直接获得一个诊断, 因在获得一个诊断时也间接的访问其他诊断
解, 故可以快速获得更多诊断. c3540、c6288 电路, 生成的子句较多, 求解冲突集和求解极大可满足子集耗时都增
加, 二者求出的解集明显减少, 但是 HSDiag 算法仍能够给出部分诊断.