Page 405 - 《软件学报》2025年第9期

4316 软件学报 2025 年第 36 卷第 9 期

粒度 1 节点 1−N 自适应 节点 1−N
时间特征 空间特征 时空特征
时间注意力 掩码注意力 图卷积
网络 拓扑结构网络 神经网络 预测结果

链路预测
GWMA
粒度 2

时间注意力 掩码注意力 图卷积 融合 稀疏惩罚
网络 拓扑结构网络 神经网络 注意力网络 损失

GWMA
粒度 3

时间注意力 掩码注意力 图卷积 真实结果
网络 拓扑结构网络 神经网络

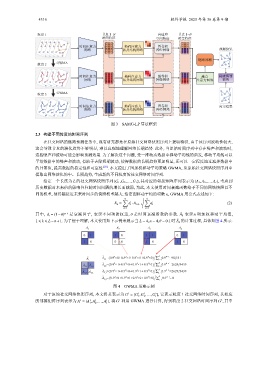
图 3 SAMG-LP 算法框架

2.3 构建不同粒度的时间序列
在社交网络的链路预测任务中, 现有研究都是在原始社交网络快照序列上提取特征, 由于该序列波动性较大,
这会导致节点的演化趋势不够明显, 难以直观地理解网络长期趋势. 此外, 当原始时间序列中存在噪声和波动时,
这些噪声和波动可能会影响预测效果. 为了解决这个问题, 受一维动态数据中移动平均线的启发, 移动平均线可以
平滑数据中的噪声和波动, 有助于去除短期波动, 使得数据的长期趋势更加明显, 还可以一定程度地过滤掉数据中
的异常值, 提高数据的稳定性和可靠性 [29] . 本文提出了图加权移动平均策略 GWMA, 从原始社交网络快照序列中
提取出网络演化的中、长期趋势, 生成新的不同粒度的社交网络时间序列.
给定一个长度为 L 的社交网络快照序列 {G 1 ,G 2 ,...,G L }, 其对应的邻接矩阵序列表示为 {A 1 ,A 2 ,...,A L }, 考虑到
历史数据对未来值的影响往往随时间间隔的增长而减弱, 为此, 本文使用时间衰减函数给予不同的网络快照以不

同的权重, 使得越接近未来时间步的快照权重越大. 给定图移动平均的项数 n, GWMA 用公式表述如下:

/
n ∑ n ∑
˜ A k = (2)
d t · A t+k−1 d t
t=1 t=1
其中, d t = (1−θ) n−t 是衰减因子, 表示不同项的权重, θ 是时间衰减函数的参数. ˜ A k 表示 项加权移动平均值,
n
˜ A k 的计算过程, 具体如图
1 ⩽ k ⩽ L−n+1. 为了便于理解, 本文使用如下示例来展示当 L = 4,n = 4,θ = 0.1 时 4 所示.

A 1 A 2 A 3 A 4
0 1 1 0 1 1 0 1
1 0 0 0 1 0 1 0
1,1 (0.9 0 0.9 1 0.9 1 0.9 0) Σ
~ ~ 3 2 1 0 4 4 t−
A = × + × + × + × 0.9 = 90 181
A 1 t= 1
~ ~ ~ 1,2 (0.9 1 0.9 0 0.9 1 0.9 1) Σ 4 4 t −
3
0
1
2
A = × + × + × + × 0.9 = 2629 3439
A 1,1 A 1,2 t= 1
2,1 (0.9 1 0.9 0 0.9 1 0.9 1) Σ
~ ~ ~ 3 2 1 0 4 4 t −
A = × + × + × + × 0.9 = 2629 3439
A 2,1 A 2,2 t= 1
~ 4 4 t−
1
0
3
2
×
× +
× +
× +
A 2,2 ( = 0.9 0 0.9 0 0.9 0 0.9 0) Σ t= 1 0. 9 = 0
图 4 GWMA 策略示例

1
1
1
1
对于原始社交网络快照序列, 本文将其表示为 G = {G ,G ,...,G }, 它表示粒度 1 社交网络时间序列, 其相应
1 2 l
1
1 1 1 1 G 利用 GWMA 进行计算, 得到粒度 2 G , 其中
2
的邻接矩阵序列表示为 A = {A ,A ,...,A }. 将 社交网络时间序列
2
1
l