Page 164 - 《软件学报》2025年第9期

李文艺 等: 增量构造式随机循环神经网络 4075

2 增量构造式随机循环神经网络

2.1 IRRNN 拓扑结构
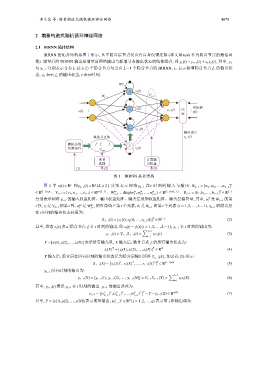
IRRNN 的拓扑结构如图 1 所示, 其中隐含层节点仅含有自身反馈连接 (本文用 tanh 作为隐含节点的激活函
数). 增量后的 IRRNN 输出是增量前网络输出与新增节点输出状态的线性组合, 即 y L (t) = y L−1 (t) + v L s L (t), 其中, y L

L L ⩾ 2) 个隐含节点与含有
与 y L−1 分别表示含有 ( L−1 个隐含节点的 IRRNN, s L 表示新增隐含节点 f L 的输出状
态, v L 表示 f L 的输出权重, 表示时刻.
t

in
W L−1
s 1 (t)
f 1
V L−1
W L−1
s 2 (t)
f 2 … y L−1 (t) 比 … 实际值
x(t) … y(t)
较
…
f L−1 s L−1 (t)
输出误差
候选节点池 e L−1 (t)
随机参数 f f f
f L
约束条件 s L (t)
C max
贪婪 计算输
选择 出权重
(1) (2) (3)
图 1 IRRNN 拓扑结构

图 1 中 x(t) ∈ R 和 y L−1 (t) ∈ R L ⩾ 2 ) 分 别 表 示 网 络 y L−1 在 t 时 刻 的 输 入 与 输 出 . W L−1 = [w 1 ,w 2 ,...,w L−1 ] T
q
p
(

∈ R (L−1)×p 、 V L−1 = [v 1 ,v 2 ,...,v L−1 ] ∈ R q×(L−1) 、 W in = diag(w ,w ,...,w in ) ∈ R (L−1)×(L−1) 、 B L−1 = [b 1 ,b 2 ,...,b L−1 ] ∈ R L−1
in
T
in

L−1 1 2 L−1
T
分别表示网络 y L−1 的输入权重矩阵、输出权重矩阵、隐含层反馈权重矩阵、隐含层偏置量, 其中, w 是 W L−1 的第
i
i
in
i
).
i 行, v i 是 V L−1 的第 列, w in i 是 W L−1 的对角线上第 i 个元素, b i 是 B L−1 的第 个元素 ( i = 1,2,...,L−1 y L−1 的隐含层
在 t 时刻的输出状态向量为:

T
S L−1 (t) = [s 1 (t), s 2 (t),..., s L−1 (t)] ∈ R L−1 (2)
(
t
),
t
其中, 状态 s i (t) 表示隐含节点 f i 在 时刻的输出, 即 s i (t) = f i (t) i = 1,2,...,L−1 y L−1 在 时刻的输出为:

∑
L−1
y L−1 (t) = V L−1 S L−1 (t) = v i s i (t) (3)
i=1
X = [x(1), x(2),..., x(N)] 表示所有输入量, X 输入后, 隐含节点 f i 的所有输出状态为:

s i (X) = [s i (1), s i (2),..., s i (N)] ∈ R N (4)
T
T
X 输入后, 隐含层在所有时刻的输出状态记为隐含层输出矩阵 S L−1 (X), 如公式 (5) 所示:

S L−1 (X) = [s 1 (X) , s 2 (X) ,..., s L−1 (X) ] ∈ R (L−1)×N (5)
T T
T
T
y L−1 所有时刻的输出为:

∑ L−1
y L−1 (X) = [y L−1 (1), y L−1 (2),..., y L−1 (N)] = V L−1 S L−1 (X) = v i s i (X) (6)
i=1
t
其中, y L−1 (t) 表示 y L−1 在 时刻的输出. y L−1 的输出误差为:

T
T
T T
e L−1 = [(e 1 L−1 ) ,(e 2 L−1 ) ,...,(e q L−1 ) ] = Y −y L−1 (X) ∈ R q×N (7)
N
其中, Y = [y(1),y(2),...,y(N)] 表示期望输出, (e j ) ∈ R (j = 1,2,...,q) 表示第 维输出误差.
j
T
L−1