Page 13 - 《软件学报》2025年第7期

2934 软件学报 2025 年第 36 卷第 7 期

′
′
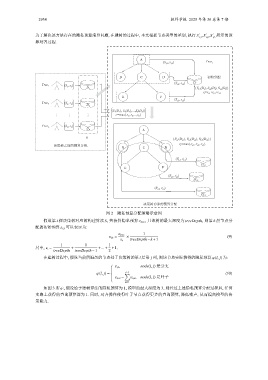
为了解决该方法存在的隐私预算浪费问题, 在建树的过程中, 本文根据节点类型的差别, 执行 S ,S ,S ′ 所示的预
i,1 i,2 i,3
算对齐过程.

A
(S i,1 , ε i,1 ) Tree i

B C D 初始分配
(S i,2 , ε i,2 ) D i
Tree 1 (S 1 , ε 1 )
D 1 {S i,1 (D i ), S i,2 (D i ), S i,3 (D i )}
ε i =ε i,1 +ε i,2 +ε i,3
E F
(S i,3 , ε i,3 )
(S 2 , ε 2 )
Tree 2
D 2
{S 1 (D 1 ), S 2 (D 2 ),...,S n (D n )}
ε=max{ε 1 , ε 2 ,...,ε n }
…
…
…
(S n , ε n )
Tree n
A
D n
D
{S ' (D ' ), S ' (D ' ), S ' (D ' )}
i,1 i,1 i,2 i,2 i,3 i,3
决策树之间的预算分配 ε ' =max{ε ' , ε ' , ε ' }
i,2
i,1
i
i,3
B C D
(S ' , ε ' )
i,1 i,1
D ' i,1
E F
(S ' , ε ' )
i,2
i,2
D ' i,2
(S ' , ε ' )
i,3
i,3
D ' i,3
决策树内部的预算分配
图 2 隐私预算分配策略示意图

假设第 i 棵决策树对应的构建算法 S i 共获得隐私预算 ε tree , 且该树的最大深度为 treeDepth, 则第 k 层节点分
配的初始预算 ε i,k 可以表示为:

ε tree 1
ε i,k = × (9)
s t treeDepth−k +1
1 1 1
其中, s t = + +...+ +1.
treeDepth treeDepth−1 2
j φ(l, j) 为:
在建树过程中, 假设当前所遍历的节点处于决策树的第 l 层第 列, 则该节点实际获得的隐私预算


 ε i,l , node(l, j) 是分支




 l−1
∑ (10)
φ(l, j) = 


 ε tree − ε i,m , node(l, j) 是叶子


m=1
如图 3 所示, 假设给予建树算法的隐私预算为 1, 模型的最大深度为 3, 则经过上述隐私预算分配过程后, 任何
支路上获得的查询预算都为 1. 同时, 对齐操作使得叶子节点获得更多的查询预算, 降低噪声, 从而提高模型的决
策能力.