Page 293 - 《软件学报》2025年第5期

刘振亚 等: SM2 数字签名算法的两方门限计算方案框架 2193

s 1 和 给 r Alice.
Bob.3 计算 s 1 = d 2 (r +w 2 ) mod q , 发送
Alice.3 计算 s = (d 1 (s 1 +w 1 )−r) mod q , 签名即为 (r, s) .

Alice Bob
m'=m||z; 计算 e=Hash(m')

随机生成或计算 w 1 ∈[1,q−1];
计算 Q 1 =[w 1 ]G
Q 1 、e

随机生成或计算 w 2 ∈[l,q−1];
−1
计算 Q=(x 1 ,y 1 )=[w 2 ]G+[d 2 ]Q 1

计算 r=(x 1 +e) mod q

计算 s 1 =d 2 (r+w 2 ) mod q
s 1 、r
计算 s=(d 1 (s 1 +w 1 )−r) mod q

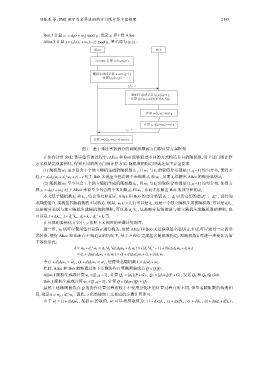
图 1 基于乘法密钥拆分的两随机数两方门限计算方案框架

在协作计算 SM2 数字签名的过程中, Alice 和 Bob 能够通过不同的方式构造各自的随机数, 对上述门限计算
方案框架完成实例化, 得到不同的两方门限计算方案. 随机数的构造应满足如下安全要求.
(1) 随机数 w 1 至少包含 1 个独立随机生成的随机数 k 1 , 且 w 1 与 k 1 的取值分布都是 [1,q−1] 均匀分布, 使得方
s = d 1 d 2 (w 2 +d w 1 +r)−r 对于 Bob w 1 , 从而无法解出
−1
程 2 来说至少包含两个未知数 d 1 和 Alice 的部分私钥 d 1 .
w 2 至少包含 1 [1,q−1] 均匀分布, 使得方
(2) 随机数 个独立随机生成的随机数 k 2 , 且 w 2 与 k 2 的取值分布都是
s 1 = d 2 (r +w 2 ) 对于 w 2 , 从而无法解出 Bob
程 Alice 来说至少包含两个未知数 d 2 和 的部分私钥 d 2 .
本文基于随机数 k 1 和 k 2 , 结合签名私钥 d , Alice 和 Bob 的部分私钥 d 1 、 d 2 以及它们的逆 d −1 、 d −1 , 进行加
1 2
或乘的组合, 实现签名随机数的不同构造. 例如, w i (i = 1,2) 可以是 k i , 这是一个独立随机生成的随机数; 可以是 d i k i ,
−1
这是部分私钥与独立随机生成随机数的乘积; 可以是 d k i , 这是部分私钥的逆与独立随机生成随机数的乘积; 也
i
−1
−1
可以是 1+d i k i 1+d k i d i +k i d +k i 等.
,
,
,
i
i
在具体的实例化方案中, s 按照上文相应的步骤计算即可.
进一步, w i 还可以使用签名私钥 d 进行构造. 虽然 Alice 和 Bob 无法获取签名私钥 d , 但是可以通过一定的形
式转换, 使得 Alice 和 Bob 在不知道 d 的情况下, 基于 P 和 G 完成签名随机数构造. 即随机数 可进一步变化为如
k
下等价形式:

−1 −1
−1
−1 −1
k = w 2 +d w 1 = d d (d 1 d 2 w 2 +d 1 w 1 ) = ((d d −1)+1)(d 1 d 2 w 2 +d 1 w 1 )
2 1 2 1 2
= (1+d)(d 1 d 2 w 2 +d 1 w 1 ) = (1+d)d 1 d 2 w 2 +(1+d)d 1 w 1 .
′ ′ ′ ′
令 (1+d)d 2 w 2 = w , (1+d)d 1 w 1 = w , 使得签名随机数 k = d 1 w +w .
2 1 2 1
此时, Alice 和 Bob 能够通过如下步骤协作计算椭圆曲线点 Q = [k]G .
Alice.1 随机生成或计算 w 1 ∈ [1,q−1] , 计算 Q 1 = [d 1 ](P+G) Q 2 = [d 1 w 1 ](P+G) , 发送 Q 1 和 Q 2 给 Bob.
,
Bob.1 随机生成或计算 w 2 ∈ [1,q−1] , 计算 Q = [d 2 w 2 ]Q 1 + Q 2 .
虽然上述椭圆曲线点 Q 的协作计算过程相较于不使用公钥 P 的计算过程有所不同, 但签名随机数的构造相
−1
s
同, 都是 k = w 2 +d w 1 . 因此, 仍然按照上文相应的步骤计算即可.
2
′ ′ 2 2
由于 w = (1+d)d i w i , 根据 w i 的取值, w 可以相应取值为: (1+d)d i k i , (1+d)d k i , (1+d)k i , (1+d)(d i +d k i ) ,
i i i i