Page 399 - 《软件学报》2024年第4期

蒋璐宇 等: 针对 MUS 求解问题的加强剪枝策略 1977

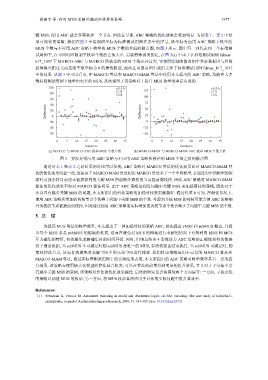
键 MSS, 使用 ABC 就会多剪枝掉一个节点. 因此在早期, ABC 策略的优化效果会更加明显. 为使表 1、表 2 中结
果可视化更清晰, 我们在图 3 中绘制横坐标为标准测试用例在表中的序号, 纵坐标为应用 ABC 策略下枚举的
MUS 个数与不应用 ABC 策略下枚举的 MUS 个数的差值的散点图, 如图 3 所示. 图中每一列代表同一个标准测
试用例下, 在不同时间限制下枚举个数的差值大小. 需要特殊说明的是, 在图 3(a) 中由于在标准测试用例 fdmus_
b17_1037 下 MARCO-ABC 与 MARCO 所枚举的 MUS 个数差异过大, 导致所绘制的散点图中其余数据因与其数
据规模差距过大而压缩至纵坐标为 0 的横线附近, 因此在该散点图中我们去掉了标准测试用例 fdmus_b17_1037
中的结果. 从图 3 中可以看出, 在 MARCO 算法和 MARCO-MAM 算法中使用本文提出的 ABC 策略, 均能在大多
数标准测试用例下枚举出更多的 MUS, 从而说明了该策略对于提升 MUS 枚举效率是有效的.

100 0.5 h 0.5 h
1 h 125 1 h
80
2 h 2 h
100
60
75
40
Difference 20 0 Difference 50
25
−20 0
−40 −25
−60 −50

0 5 10 15 20 25 30 35 0 5 10 15 20 25 30 35
Instances Instances
(a) MARCO 与 MARCO-ABC 枚举 MUS 个数差值 (b) MARCO-MAM 与 MARCO-MAM-ABC 枚举 MUS 个数差值
图 3 算法分别应用 ABC 策略与不应用 ABC 策略所枚举的 MUS 个数差值的散点图

通过对表 1 和表 2 之间结果的对比可以发现, ABC 策略对 MARCO 算法的优化效果比对 MARCO-MAM 算
法的优化效果明显一些, 这是由于 MARCO-MAM 算法相比 MARCO 算法多了一个中间模型, 在通过对中间模型的探
索时可能会将目前还未被探索到的关键 MSS 所能额外剪枝的节点提前剪枝掉, 因此 ABC 策略对 MARCO-MAM
算法的优化效果不如对 MARCO 算法明显. 由于 ABC 策略是利用问题中关键 MSS 来加强剪枝的策略, 因此对于
本身具有越多关键 MSS 的问题, 本文所提出的剪枝策略的加强剪枝效果就越好. 通过性质 4 可知, 在最优情况下,
使用 ABC 策略所增加的剪枝节点个数等于问题中关键 MSS 的个数. 考虑到其他 MSS 的剪枝可能会使 ABC 策略额
外剪枝的节点被提前剪枝掉, 因此通过使用 ABC 策略而实际增加的剪枝节点个数会略小于问题中关键 MSS 的个数.

5 总 结

为提高 MUS 算法的枚举效率, 本文提出了一种加强剪枝的策略 ABC, 首先提出 cMSS 和 subMUS 概念, 并提
出每个 MUS 必是 subMUS 的超集的性质, 进而在避免对 MCS 的碰集进行求解的情况下有效利用 MUS 和 MCS
互为碰集的特征, 有效避免求解碰集时的时间开销. 同时, 归纳总结出 4 条性质为 ABC 策略的正确性和有效性提
供了理论依据, 当 subMUS 不可满足时则 subMUS 是唯一的 MUS, 算法将提前结束执行; 当 subMUS 可满足时, 则
剪枝掉此节点, 从而有效避免对求解空间中的冗余空间进行搜索. 我们将该策略应用于已有的 MARCO 算法和
MARCO-MAM 算法, 通过在标准测试用例下的实验结果表明, 本文所提出的 ABC 策略对枚举效率具有一定的提
升效果. 该策略与使用极大化模型的算法结合起来, 可以在算法的前期得到明显的提升效果, 并且对于子句集中含
有越多关键 MSS 的实例, 该策略对算法的优化效果越佳. 后续的研究重点将围绕两个方向展开: 一方面, 寻找更优
的策略以加速 MUS 的枚举; 另一方面, 将 MUS 枚举算法应用于具体的实际问题中提升其效率.

References:
[1] Sebastiani R, Vescovi M. Automated reasoning in modal and description logics via SAT encoding: The case study of K(m)/ALC-
satisfiability. Journal of Artificial Intelligence Research, 2009, 35: 343–389. [doi: 10.1613/jair.2675]