Page 371 - 《软件学报》2024年第4期

徐怡 等: 基于遗传算法的划分序乘积空间问题求解层选择 1949

从图 1 可以看出, 划分序乘积空间中有 8 个问题求解层, 不仅可以从多个视角解决问题, 还可以从多个层次解
决问题. 根据实际诊断需要, 医生可以在不同视角和视角的不同层次之间灵活选择和变换, 从而获得更加准确的诊
断结果.
2 两阶段自适应遗传算法

由于划分序乘积空间是格结构, 因此解空间较大, 在划分序乘积空间中找到合适的问题求解层是一个 NP 难
问题. 遗传算法是处理 NP 难问题的常用方法 [28,29] , 但经典遗传算法存在收敛速度慢、容易陷入局部最优等问题.
Mathias 等人 [30] 提出了一种平行两阶段多种群遗传算法, 其在第 1 阶段使用多种群遗传算法来寻找优良的个体, 并
将这些个体作为第 2 阶段的初始种群来缩小解空间范围. 但是该方法基于多种群遗传算法, 因此算法复杂度较高.
此外, 该算法没有考虑种群的多样性会随着种群进化迭代次数的增加而变化, 因此其选择算子、交叉算子以及变
异算子在整个种群进化迭代期间是固定不变的. 为此, 本文在上述算法的基础上, 提出一种两阶段自适应遗传算
法 TSAGA. 算法第 1 阶段利用具有较少迭代次数的经典遗传算法, 从划分序乘积空间中选择问题求解层, 每一次
迭代都将当前种群中最好的个体保存在个体集合 POP 中. 算法第 2 阶段, 首先, 将 POP 中保存的个体作为第 2 阶
段初始种群的一部分, 其余染色体仍然按照传统方法随机产生, 从而使第 2 阶段获得较优的初始种群, 优化解空
间. 然后, 在第 2 阶段中, 考虑种群的多样性会随着种群进化迭代次数的增加而变化, 定义随当前种群进化迭代次
数动态变化的自适应选择算子和自适应交叉算子. 最后, 为了增强算法跳出局部最优解的能力, 定义自适应大变异
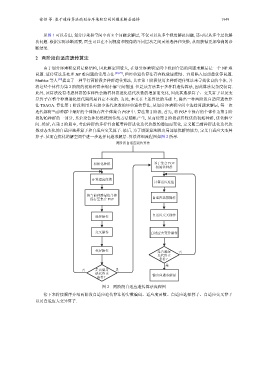
算子. 从而在优化的解空间中进一步选择问题求解层. 算法详细流程图如图 2 所示.

两阶段自适应遗传算法

初始化种群 基于集合 POP
初始化种群

计算适应度值
计算适应度值

将当前种群最优个体
保存至集合 POP 自适应选择操作

选择操作 自适应交叉操作

交叉操作 自适应大变异操作

变异操作 是否满足 否
迭代终止
条件？
是
否 是否满足 是
迭代终止 输出问题求解层
条件？

图 2 两阶段自适应遗传算法流程图

接下来将按顺序介绍两阶段自适应遗传算法的实数编码、适应度函数、自适应选择算子、自适应交叉算子
以及自适应大变异算子.