Page 10 - 《软件学报》2021年第12期

3674 Journal of Software 软件学报 Vol.32, No.12, December 2021

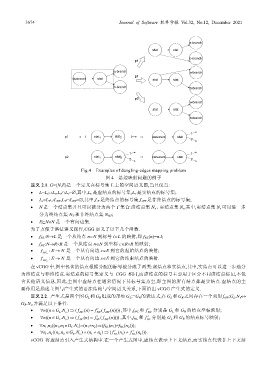
Fig.4 Examples of dangling-edges mapping problem
图 4 悬边映射问题的例子
定义 2.1. G=(N,E)是一个定义在标号集 L 上的空间语义图,当且仅当:
• L=L v ∪L r ,L v ∩L r =∅,其中,L v 是虚结点的标号集,L r 是实结点的标号集;
• L r =L T ∪L NT ,L T ∩L NT =∅,其中,L T 是终结点的标号集,L NT 是非终结点的标号集;
• N 是一个结点集并且可以被分为两个子集合:虚结点集 N v 、实结点集 N r ,其中,实结点集 N r 可以进一步
分为终结点集 N T 和非终结点集 N NT ;
• E⊆N×N 是一个有向边集.
为了方便于语法语义操作,CGG 定义了以下几个函数.
• f NL :N→L 是一个从结点 n∈N 到标号 l∈L 的映射,即 f NL (n)=n.l;
• f NC :N→R×R 是一个从结点 n∈N 到坐标 c∈R×R 的映射;
• f EN s : E → N 是一个从有向边 e∈E 到它的起始结点的映射;
• f EN e : E → N 是一个从有向边 e∈E 到它的结束结点的映射.
在 vCGG 中,图中包含的结点根据分配的标号被分成了两类:虚结点和实结点,其中,实结点可以进一步地分
为终结点与非终结点.实结点的标号集定义与 CGG 相同,而虚结点的标号主要用于区分不同虚结点标记,不包
含其他语义信息,因此,主图中虚结点在通常情况下其标号集为空,即主图的所有结点都是实结点.虚结点的主
要作用是描述主图与产生式的语法结构与空间语义关系,下面给出 vCGG 产生式的定义.
定义 2.2. 产生式是两个图 G L 和 G R 组成的形如 G L :=G R 的表达式,在 G L 和 G R 之间存在一个双射 f NN :G L .N v ↔
G R .N v ,并满足以下条件.
(( ∈
• ∀ nn G .N ⇒ ) ( f ( )n = f ′ ( f ( ))))n ,其中,f NC 和 f ′ 分别是 G L 和 G R 的结点坐标映射;
L v NC NC NN NC
• ∀ nn G∈ (( L .N ⇒ v ) ( f NL ( )n = f ′ NL ( f NN ( ))))n ,其中,f NL 和 f ′ 分别是 G L 和 G R 的结点标号映射;
NL
• ∀n 1 ,n 2 ((n 1 ,n 2 ∈G L .N v )∧(n 1 ≠n 2 )⇒(f NL (n 1 )≠f NL (n 2 )));
• ∀ n 1 ,n 2 (( ,n n ∈ 1 2 G R .N ∧ v ) (n ≠ 1 n 2 ) ⇒ ( f ′ NL ( )n ≠ 1 f ′ NL ( )))n 2 .
vCGG 将虚结点引入产生式结构中.在一个产生式图中,虚结点表示上下文结点,而实结点代表非上下文结