Page 281 - 《软件学报》2021年第9期

沈军 等:基于卷积神经网络的低嵌入率空域隐写分析 2905

值大的做为最终结果.

训练样本

噪声残差提取

卷积操作
提取隐写特征

反 全连接层 正
向 向
传 传
播 播
输出层

嵌密图像
输出值
是 与目标值偏差
超过阈值?
否 噪声残差提取
网络模型

分类

Stego/Cover

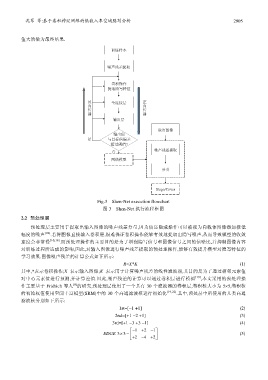
Fig.3 Shen-Net execution flowchart
图 3 Shen-Net 执行流程框图
2.2 预处理层
预处理层主要用于提取出输入图像的噪声残差分量,因为信息隐藏操作可以被视为向载体图像添加极低
幅度的噪声 [22] .若将图像直接输入卷积层,很难保证卷积操作能够有效地提取出隐写噪声,从而导致模型的收敛
速度会非常慢 [10,16] .而预处理操作的主要目的是为了增强隐写信号和图像信号之间的信噪比,并抑制图像内容
对训练过程所造成的影响,因此,对输入图像进行噪声残差提取的预处理操作,能够有效提升模型对隐写特征的
学习效果.图像噪声残差的计算公式如下所示:
R=X*K (1)
其中,*表示卷积操作;X 表示输入图像;K 表示用于计算噪声残差的线性滤波器,其目的是为了通过相邻元素值
对中心元素值进行预测,并计算差值.因此,噪声残差的计算可以通过卷积层进行模拟 [19] ,本文采用的预处理操
[8]
作主要基于 Fridrich 等人 的研究,预处理层使用了一个具有 30 个滤波器的卷积层,卷积核大小为 5×5,卷积核
的初始权值使用空间丰富模型(SRM)中的 30 个高通滤波核进行初始化 [19,22] .其中,预处层中所使用的几类高通
滤波核分别如下所示:
1st=[−1 +1] (2)
2nd=[+1 −2 +1] (3)
3rd=[+1 −3 +3 −1] (4)
− 1 + ⎡ 2 − 1⎤
33 =
EDGE × ⎢ ⎥ (5)
⎣ + 2 − 4 + 2 ⎦