Page 153 - 《软件学报》2021年第9期

陈佳楠 等:基于多核 CPU 的表约束并行传播模式研究 2777

多个线程在并行执行对不同表约束的并行过滤算法时,可能会同时过滤同一个变量 x 的论域 bitdom(x)(算
法 9 第 6 行),也可能会同时更新约束位标识 tableMask(算法 9 第 11 行),所以我们对这两种操作采用了非阻塞同
步方式,通过比较并替换(compare and swap,简称 CAS)实现,以确保并行过滤算法的正确性.
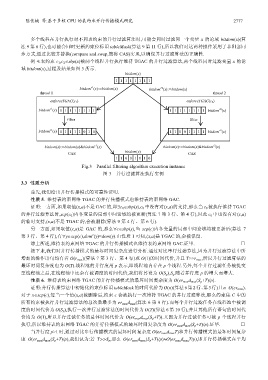
例 4:表约束 c 1 ,c 2 ∈sbp(x)被两个线程并行执行维持 TGAC 的并行过滤算法,两个线程同时过滤变量 x 的论
域 bitdom(x),过程及结果如图 3 所示.
bitdom(x)

1 1 1 1 1 1 1 1

c1
c2
bitdom (x):ൌbitdom(x) bitdom (x):ൌbitdom(x)
thread 1 thread 2

enforceTGAC(c 1) enforceTGAC(c 2)

c1
c2
bitdom (x) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 bitdom (x)

filter filter

c1
c2
bitdom (x) 1 1 1 1 1 0 1 0 1 1 0 0 1 1 1 1 bitdom (x)

c2
c1
bitdom(x):ൌbitdom(x)&bitdom (x) bitdom(x):ൌbitdom(x)&bitdom (x)

bitdom(x)
CAS CAS

1 1 0 0 1 0 1 0
Fig.3 Parallel filtering algorithm execution instance
图 3 并行过滤算法执行实例
3.3 性质分析
首先,我们给出并行传播模式的可靠性证明.
性质 5. 维持表约束网络 TGAC 的并行传播模式也维持表约束网络 GAC.
证明:一方面,如果取值(x,a)不是 GAC 的,即∃c 0 ∈sbp(x),c 0 中没有对(x,a)的支持,那么当 c 0 被执行维持 TGAC
的并行过滤算法时,scp(c 0 )内各变量的局部中间论域均被更新(算法 7 第 3 行、第 4 行),因此 c 0 中也没有对(x,a)
的临时支持,(x,a)不是 TGAC 的,会被删除(算法 9 第 4 行、第 6 行).
另一方面,如果取值(x,a)是 GAC 的,那么∀c∈sbp(x),当 scp(c)内各变量的局部中间论域均被更新后(算法 7
c
第 3 行、第 4 行),有∀y∈scp(c),dom (y)=dom(y).由性质 1 可知,(x,a)是 TGAC 的,会被保留.
综上所述,维持表约束网络 TGAC 的并行传播模式也维持表约束网络 GAC.证毕. □
接下来,我们对并行传播模式的最坏时间复杂度进行分析.通过对比串行过滤算法,因为并行过滤算法中所
增加的操作语句均有着 O(r max )(算法 7 第 3 行、第 4 行)或 O(1)的时间代价,并且 T>>r max ,所以并行过滤算法的
最坏时间复杂度也为 O(T).线程池的并行度用 p 表示,即线程池内存在 p 个线程.另外,每个并行过滤任务被提交
至线程池之后,在线程池中还会有被调度的时间代价,我们将其设为 O(S p ),S p 随着并行度 p 的增大而增大.
性质 6. 维持表约束网络 TGAC 的并行传播模式的最坏时间复杂度为 O(er max d max (S p +T)/p).
证明:并行传播算法中初始化约束位标识 tableMask 的时间代价为 O(n)(算法 6第 2 行、第 3行)且 n=O(er max ).
对于 x∈scp(c),每当一个值(x,a)被删除后,约束 c 会被执行一次维持 TGAC 的并行过滤算法,那么约束集 C 中的
所有约束被执行并行过滤算法的总次数最多为 er max d max (算法 6 第 9 行).而每个并行过滤任务在线程池中被调
度的时间代价为 O(S p ),执行一次并行过滤算法的时间代价为 O(T)(算法 6 第 10 行),并且其他所有语句的时间代
价均为 O(1),所以并行过滤任务的总体时间代价为 O(er max d max (S p +T)).又因为并行过滤任务可被 p 个线程并行
执行,所以维持表约束网络 TGAC 的并行传播模式的最坏时间复杂度为 O(er max d max (S p +T)/p).证毕. □
当并行度 p>1 时,通过对比串行传播模式的最坏时间复杂度 O(er max d max T)和并行传播模式的最坏时间复杂
度 O(er max d max (S p +T)/p),我们认为:若 T>>S p ,那么 O(er max d max (S p +T)/p)≈O(er max d max T/p),即并行传播模式在平均