Page 135 - 《软件学报》2021年第8期

杨世贵 等:基于强化学习的温度感知多核任务调度 2417

们使用梯度下降和以下损失函数来更新其参数θ:
2
L(θ)=E[(r+γ maxQ(s′,a′,θ)−Q(s,a,θ)) ] (12)
其中,r 为状态 s 下执行动作 a 的奖励,r+γ maxQ(s′,a′,θ)为目标 Q 值,而 Q(s,a,θ)是真实的 Q 值.Q-Learning 通过
目标值和真实值之间的误差期望值建立损失函数.
4.4 Q-Learning参数设置

(1) 学习率
Q-Learning 中,学习率表示了 Q 值更新的幅度,决定了算法的收敛速度和最终的收敛效果.学习率较大时,
算法收敛较快,但一定程度上会影响性能 [30] .所以通常初始化一个较大的学习率,随着算法运行次数的增加,逐
步缩小学习率,从而使算法收敛速度较快且最终性能较好.在 ReLeTA 中,我们通过实验来经验性地确定最佳学
习率.实验平台与第 4 节中的一致.通过反复调度同一个任务,来观察不同的学习率下算法的收敛效率和对温度
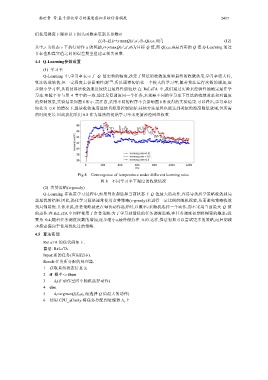
的控制效果,实验结果如图 8 所示.需注意,采用不同的程序不会影响图 8 所获得的实验结果.可以看出,学习率初
始化为 0.8 的情况下,算法收敛速度最快且温度控制较好;其他方法最终也能达到类似的温度降低效果,但所需
的时间更长.因此我们采用 0.8 作为算法的初始学习率来更新神经网络权重.

Fig.8 Convergence of temperature under different learning rates
图 8 不同学习率下温度的收敛情况
(2) 贪婪策略(ε-greedy)
Q-Learning 在决策学习过程中,如果每次都选择当前状态下 Q 值最大的动作,容易导致所学策略收敛到局
部最优的结果.因此,强化学习算法通常使用贪婪策略(ε-greedy)来进行一定比例的随机探索,从而避免策略收敛
到局部最优.具体来说,贪婪策略就是在每次动作选择时,以概率ε来随机选择一个动作,而不采用当前最大 Q 值
的动作.在 ReLeTA 中同样使用了贪婪策略:为了学习到最优的任务调度策略,在任务调度初期将探索的概率ε设
置为 0.4;随着任务调度次数的增加,逐步缩小ε,最终保持在 0.03.这样,算法初期可以尝试更多的策略,而后期减
少探索偏向于使用优化过的策略.
4.5 算法实现
ReLeTA 的伪代码如下.
算法. ReLaTA.
Input:新的任务(应用程序).
Result:任务所分配的处理器.
1 获取系统状态信息 S t
2 if 概率<ε then
3 A t (在动作空间中随机选择动作)
4 else
5 A t =argmaxQ(S t ,a t ,θ)(选择 Q 值最大的动作)
6 使用 CPU_affinity 将任务分配到处理器 A t 上