Page 269 - 《高原气象》2025年第3期

3 期 苗 芮等：基于深度学习的多气象要素影响的供热负荷预测模型研究 827

图4 2021 -2022年采暖季逐小时供热负荷与各气象要素的时滞相关系数
其中横坐标表示超前24 h到滞后24 h， 0表示同时相关， 黑色虚线表示95%显著性检验的临界值
Fig. 4 The lagged correlation coefficients of hourly heating load with various meteorological factors during the 2021 -2022
heating season. The horizontal axis represents a range from 24 hours ahead to 24 hours behind， with 0 indicating
simultaneous correlation， and the black dashed line indicating the threshold for the 95% significance test
和风速与供热负荷的相关性因月份而异， 总体较 7中（a）~（h）分别代表输入数据集A至数据集H， 包含
弱。时滞相关分析表明， 供热负荷与气温在滞后1~ 了不同的要素， 其中数据集A表示仅输入历史供热负
2 h 及同时的相关性最强。总体来看， 供热负荷与 荷和平均气温， 数据集H表示输入历史供热负荷、平
气象因子的关系具有明显的季节差异。 均气温、风速、相对湿度和太阳辐射， 具体见表1， 横
3. 3 供热负荷预测模型实验结果 坐标 X_Y 表示不同的滑动窗口 X 和隐含层数 Y 的
通过训练和验证供热负荷预测的每个模型， 共 NARX神经网络模型）。结果显示， 滑动窗口长度为
得到480组实验结果， 其RMSE、MAE、SMAPE指标 8 h 且隐含层数为 4 层的 NARX 神经网络预测模型
的箱线图如图5~7所示（为了更好地比较结果， 仅展 （NARX_8_4）在大多数数据集上的评价指标的分布
示滑动窗口为4 h和8 h的实验结果， 因滑动窗口2 h 最为集中， 并具有最小的中位数。因此， 可以得出
的模型误差分布较为分散， 并存在较多异常值； 图5~ “NARX_8_4”模型为逐小时负荷预测的最佳模型。

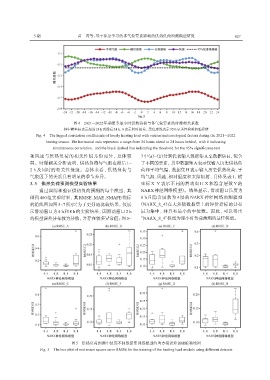
图5 供热负荷预测中使用不同数据集训练模型的均方根误差RMSE箱线图
Fig. 5 The box plot of root mean square error RMSE for the training of the heating load models using different datasets