Page 267 - 《高原气象》2025年第3期

3 期 苗 芮等：基于深度学习的多气象要素影响的供热负荷预测模型研究 825
常数据进行处理， 在本研究中主要是通过相邻数据
的平均值来修正或补全异常数据。
2. 2. 2 NARX神经网络模型数据集构建
为了考察气温、风速、湿度、太阳辐射对供热负
荷的影响， 构建数据集如表 1 所示。在逐时供热负
荷的模型建立过程中， 考虑到气象要素的季节变
化， 故选择每月序列的前 80% 为训练集， 后 20% 为
测试集。

表1 多要素数据集
Table 1 Multi-factor datasets
历史供热 平均 太阳 平均 相对
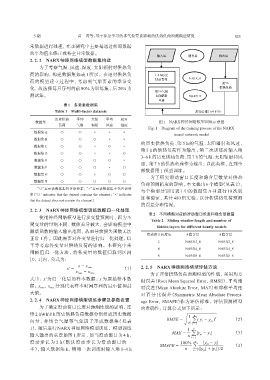
数据集 图1 NARX神经网络模型训练示意图
负荷 气温 辐射 风速 湿度
Fig. 1 Diagram of the training process of the NARX
数据集A ○ ○ × × ×
neural network model
数据集B ○ ○ ○ × ×
的历史供热负荷、第 5 h 的气温、太阳辐射和风速，
数据集C ○ ○ × ○ ×
第 5 h 的供热负荷作为输出； 第二次训练时输入第
数据集D ○ ○ × × ○
3~6 h的历史供热负荷、第7 h的气温、太阳辐射和风
数据集E ○ ○ ○ ○ ×
速， 第 7 h的供热负荷作为输出； 以此类推， 直到全
数据集F ○ ○ ○ × ○
部数据用于模型训练。
数据集G ○ ○ × ○ ○
为了研究滑动窗口长度和隐含层数量对供热
数据集H ○ ○ ○ ○ ○
负荷预测精度的影响， 本文提出 6 个模型（见表 2），
“○”表示该数据集包含该要素， “×”表示该数据集不包含该要
每个模型分别用表 1 中的数据集 A-H 进行 10 次训
素（'○ ' indicates that the dataset contains the element； '× ' indicates
练和验证， 共计 480 组实验， 以分析供热负荷预测
that the dataset does not contain the element）
的误差分布情况。
2. 2. 3 NARX神经网络模型训练数据归一化处理
表2 不同模型对应的滑动窗口长度和隐含层数量
使用神经网络模型进行多变量预测时， 因为不
Table 2 Sliding window length and number of
同变量的量纲不同， 数值差异较大， 会影响模型中 hidden layers for different hourly models
激活函数的输入输出范围， 从而导致损失函数无法
滑动窗口长度/h 4隐含层 8隐含层
正常工作。因此需要对各变量进行归一化处理， 以
2 NARX2_4 NARX2_8
平等考虑各变量对供热负荷的影响。本研究中采
4 NARX4_4 NARX4_8
用极值归一化方法， 将各变量的数值归算到区间
8 NARX8_4 NARX8_8
［0， 1］内， 公式为：
x' = x - x min （1） 2. 2. 5 NARX神经网络模型评估方法
x max - x min
为了评估供热负荷预测模型的性能， 采用均方
式中： x'为归一化后的样本数据； x 为原始样本数 根误差（Root Mean Squared Error， RMSE）、平均绝
据； x min ， x max 分别代表样本时间序列的最小值和最
对误差（Mean Absolute Error， MAE）和对称平均绝
大值。 对 百 分 比 误 差（Symmetric Mean Absolute Percent‐
2. 2. 4 NARX神经网络模型训练步骤及参数设置 age Error， SMAPE）作为评估标准， 评估预测模型
为了确定滑动窗口长度对预测性能的影响， 连 的准确性， 计算公式如下所示：
续 2 h\4 h\8 h 历史供热负荷数据分别组成历史数据 1 n
向量， 并结合气温等气象因子形成数据集（见表 RMSE = n ∑ ( y i - y pi ) 2 （2）
i = 1
1）， 随后进行 NARX神经网络模型训练。模型训练 1 n
MAE = ∑ |y pi - y i | （3）
输入输出的示意如图 1 所示， 如当滑动窗口为 4 h， n
i = 1
滑动步长为 2 h（默认滑动步长为滑动窗口的一 100% n |y pi - y i |
SMAPE = ∑ （4）
半）， 输入数据集 E， 则第一次训练时输入第 1~4 h n i = 1 (|y pi | + |y i |)/2