Page 35 - 《爆炸与冲击》2025年第9期

第 45 卷 郭 丁，等： 基于大型激波管氢氧爆轰驱动方式产生冲击波波形调控的数值模拟 第 9 期

1.4 模型可靠性验证与收敛性分析

为验证本文中所建数值模型的可靠性，利
5.0
用该模型对 Yamanaka 等 [26] 利用长度为 4.5 m、
Experiment [26]
直径为 50 mm 的爆轰驱动管开展的氢氧爆轰驱 4.0 Simulation
动实验进行数值模拟。数值模拟得到的爆轰压
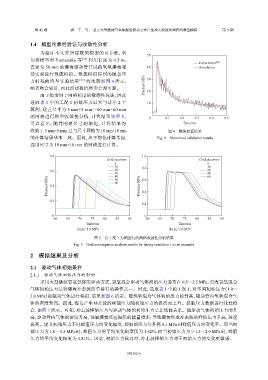
力时程曲线与实验结果 [26] 的比较如图 4 所示， 3.0
两者吻合较好，因此所建数值模型合理可靠。 Pressure/MPa 2.0
由于模型对于网格精度的敏感性较强，因此
选取表 1 中的工况 1 初始压力最大与最小 2 个 1.0
算例，建立尺寸为 5 mm×5 mm～60 mm×60 mm
的网格进行模型收敛性分析，计算结果见图 5。 0 0.1 0.2 0.3 0.4 0.5
可 以 看 出 ， 随 着 网 格 尺 寸 的 细 化 ， 计 算 结 果 均 Time/ms
收敛于 5 mm×5 mm，且与尺寸网格为 10 mm×10 mm 图 4 数值验证结果
的计算结果基本一致。因此，出于简化计算考虑， Fig. 4 Numerical validation results
选用尺寸为 10 mm×10 mm 的网格进行计算。

0.8 1.0

Grid size/mm Grid size/mm
5 5
10 0.8 10
0.6 20 20
30 40
40
60
Pressure/MPa 0.4 60 Pressure/MPa 0.6
50
0.4
0.2
0.2

0 0
60 65 70 75 80 85 90 60 65 70 75 80 85 90
Time/ms Time/ms
(a) p 0 =1.0 MPa (b) p 0 =2.0 MPa
图 5 以工况 1 为例进行的网格收敛性分析结果
Fig. 5 Grid convergence analysis results by taking condition 1 as an example

2 模拟结果及分析

2.1 驱动气体初始条件

2.1.1 驱动气体初始压力的影响
采用大型激波管氢氧爆轰驱动方式，氢氧混合驱动气体初始压力通常在 0.5～2.5 MPa，更改氢氧混合
气体初始压力是对爆轰冲击波简单易行的操作之一。因此，选取表 1 中的工况 1，对不同初始压力（1.0～
2.0 MPa）的驱动气体进行模拟，结果如图 6 所示。随氢氧混合气体初始压力的升高，驱动管内氢氧混合气
体的密度升高。因此，爆轰产生冲击波的峰值压力随初始压力的提高而上升。提取压力数据进行线性拟
合，如图 7 所示。可知，冲击波峰值压力与驱动气体的初始压力呈非线性关系。随驱动气体初始压力的升
高，驱动管内气体的密度升高，氢氧爆轰反应提供的能量增多，导致爆轰形成冲击波的峰值压力升高，波速
提高。定义初始压力不同峰值压力的变化幅度，即初始压力每升高 0.1 MPa 时峰值压力的变化率。而当初
始压力为 1.0～1.5 MPa 时，峰值压力的平均变化幅度仅为 1.62%，而当初始压力为＞1.5～2.0 MPa 时，峰值
压力的平均变化幅度为 4.81%。因此，初始压力较高时，冲击波峰值压力对于初始压力的变化更敏感。

092102-6