Page 140 - 《爆炸与冲击》2025年第9期

第 45 卷 焦俊杰，等： 基于水下爆炸的爆轰产物JWL状态方程确定方法研究 第 9 期

3 水下爆炸试验法验证

为进一步分析水下爆炸法确定的 JWL 状态参数的准确性，利用测定得到的 JWL 状态方程参数对
水下爆炸的气泡动力学过程进行计算。从 2.2 节的试验可知，炸药爆轰结束后，爆轰产物迅速占据了
炸药的原有体积，随即从静止开始快速膨胀。从炸药的爆轰过程来看，初始气泡可视为一个与装药体
积 相 同 的 球 体 ， 其 半 径 为 R ， 初 始 速 度 为 零 。 Shan 等 [18] 和 Wang 等 [19] 发 现 ， 当 装 药 表 面 压 力 达 到
0
9.8～19.6 GPa 时，与储存在流体中的压缩能相比，动能和压力位能是装药附近流体能量的主要组成部
分，Rayleigh-Plesset 方程可以描述气泡加速膨胀的运动过程。由于压力波的传播速度不是无限的，且流
体的比容在发生变化时会储存一定的压缩能，当研究气泡在整个脉动周期内的运动特性时，需要考虑流
体的压缩性以减小计算的误差。因此，对气泡动力学过程进行计算时，首先利用 Rayleigh-Plesset 方程 [18-19]
计算气泡的初始加速膨胀过程，随后，利用气泡在可压缩流体中的动力学方程 [15] 对后续的气泡减速膨胀
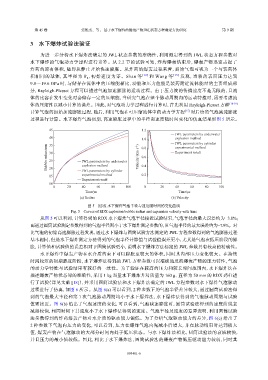
过程进行计算。水下爆炸气泡初期，高速膨胀过程中的半径和速度随时间变化的仿真结果如图 5 所示。

45 1.2

JWL parameters by underwater
40 1.0 explosion method
JWL parameters by cylinder
35
Bubble radius/mm 30 JWL parameters by underwater Velocity/(km·s −1 ) 0.8 Experiment result
experimental method
0.6
25
explosion method
0.4
20
experimental method
15 JWL parameters by cylinder 0.2
Experiment result
10
0 20 40 60 80 100 0 20 40 60 80 100
Time/μs Time/μs
(a) Radius (b) Velocity

图 5 RDX 水下爆炸气泡半径与速度随时间的变化曲线
Fig. 5 Curves of RDX explosion bubble radius and expansion velocity with time
从图 5 可以看到，计算得到的 RDX 水下爆炸气泡半径接近试验结果，气泡半径的最大误差约为−3.8%；
而通过圆筒试验测定参数得到的气泡半径则小于水下爆炸测定参数的，且气泡半径的最大误差约为−7.9%。对
比气泡的初始高速膨胀过程发现，通过水下爆炸与圆筒试验方法测定的 JWL 方程参数得到的气泡膨胀过程
基本相同，但是水下爆炸测定方法得到的气泡半径计算值与试验值误差更小，尤其是气泡在低压阶段的膨
胀，计算值和试验值的误差相对于圆筒试验更小，说明水下爆炸方法标定的 JWL 参数具有较高的精确性。
水下爆炸中爆轰产物在水介质约束下可以膨胀至较大的体积，同时其内部压力变化较大。在持续
时间较短的初期膨胀阶段，水下爆炸法得到的 JWL 方程参数可以准确地反映爆轰产物的压力特性，气泡
的动力学特性与试验结果有较好的一致性。为了验证在较高的压力和较长时间范围内，水下爆炸法在
描述爆轰产物状态时的准确性，采用 1 kg 当量水下爆炸井对质量为 160 g、直径为 50 mm 的 RDX 药柱进
行了试验（详见文献 [18]），并采用圆筒试验法和水下爆炸法确定的 JWL 方程参数对水下爆炸气泡脉动
过程进行了仿真，如图 6 所示。从图 6(a) 可以看到，2 种参数下的气泡半径差异较大，通过圆筒试验法得
到的气泡最大半径和第 1 次气泡脉动周期均小于水下爆炸法，水下爆炸法得到的气泡脉动周期与试验
值更接近。图 6(b) 给出了气泡速度的变化，可以看到，气泡减速膨胀时，圆筒试验法得到的速度曲线衰
减得较快，相同时间下其速度小于水下爆炸法得到的速度。气泡半径及速度的差异表明，利用圆筒试验
法参数得到的炸药爆轰产物对水介质的驱动能力偏低。为了分析气泡驱动能力的差异，图 6(c) 给出了
2 种参数下气泡内压力的变化，可以看到，压力在爆炸气泡内先减小后增大，并在脉动结束时达到极大
值，爆轰产物在气泡脉动的大部分时间内处于低压状态。与水下爆炸法相比，圆筒试验法的衰减较快，
并且压力的最小值较低。因此，相比于水下爆炸法，圆筒试验法的爆轰产物低压驱动能力较弱，同时其

093401-6