Page 105 - 《爆炸与冲击》2025年第6期

第 45 卷 蔚立元，等： 动态恒速剪切下砂岩粗糙结构面的力学行为及嗣后渗流特性 第 6 期

72 36

R 0 =8.87 30 R 0 =8.87
R 0 =12.43
R 0 =12.43
60
Surface degradation ratio/% 48 R 0 =18.38 η/% 24 R 0 =18.38
R 0 =15.60
R 0 =15.60
36
18
24
12
12
0 6 0
40 60 80 100 120 140 160 180 200 220 40 60 80 100 120 140 160 180 200 220
Shear velocity/(mm·s ) Shear velocity/(mm·s )
−1
−1
(a) Surface degradation ratio (b) Joint roughness coefficient degradation ratio
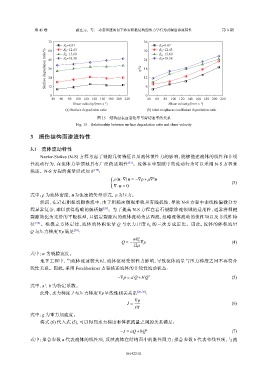
图 15 结构面表面退化率与剪切速率的关系
Fig. 15 Relationship between surface degradation ratio and shear velocity

3 损伤结构面渗流特性

3.1 流体流动特性
Navier-Stokes (N-S) 方程考虑了裂隙几何特征以及流体惯性力的影响，能够描述流体的线性和非线
性流动行为，在流体力学领域具有广泛的适用性 [23] 。流体在单裂隙中的流动行为可以采用 N-S 方程来
描述。N-S 方程的张量形式如下 [30] ：
® 2
ρ(u·∇)u = −∇p+µ∇ u
(3)
∇·u = 0
式中：ρ 为流体密度， u 为流速的矢量形式， p 为压力。
然而，在岩石粗糙裂隙渗流中，由于粗糙面微观形貌具有随机性，导致 N-S 方程中非线性偏微分方
程异常复杂，难以获得精确的解析解 [29] 。为了提高 N-S 方程在岩石裂隙渗流领域的适用性，通常将粗糙
裂隙简化为光滑的平板模型，且假定裂隙内的流体流动为达西流，忽略流体流动的惯性项以及非线性特
征 [30] 。根据立方体定律，流体的体积流量 Q 与水力开度 b 的三次方成正比。因此，流体的体积流量
h
Q 与压力梯度 ∇p 满足 [30] ：
wb 3 h
Q = − ∇p (4)
12µ
式中：w 为裂隙宽度。
地下工程中，当流体流速较大时，流体流动受惯性力影响，导致流体流量与压力梯度之间不再符合
线性关系。因此，采用 Forchherimer 方程描述流体的非线性流动状态：
′
′
−∇p = a Q+b Q 2 (5)
式中，a′、b′为特定系数。
此外，水力梯度 J 与压力梯度 ∇p 呈线性相关关系 [28, 30] ：

∇p
J = (6)
ρg
式中：g 为重力加速度。
将式 (6) 代入式 (5)，可以得到水力梯度和体积流量之间的关系满足：

−J = aQ+bQ 2 (7)
式中：拟合参数 a 代表流体的线性项，反映流体在结构面中的黏性阻力；拟合参数 b 代表非线性项，与流

061422-11