Page 33 - 《爆炸与冲击》2023年第2期

第 43 卷 杨 鑫，等： 单晶与纳米多晶锡层裂的分子动力学研究 第 2 期

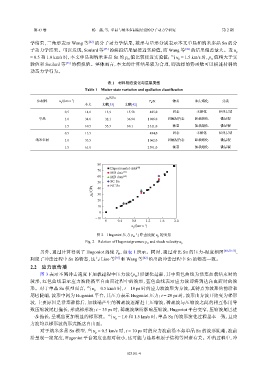
学结果，三角形表示 Wang 等 [42] 的分子动力学结果，菱形与星形分别表示本文单晶和纳米多晶 Sn 的分
子动力学结果。可以发现，Soulard 等 [35] 的模拟结果最接近实验值，而 Wang 等 [42] 的结果偏差最大。当 u
p
= 0.5 和 1.0 km/s 时，本文单晶和纳米多晶 Sn 的 p 值比较接近实验值；当 u = 1.5 km/s 时，p 值稍大于实
H
H
p
验值和 Soulard 等 [35] 的模拟值。整体而言，本文的计算结果较为合理，即选择的势函数可以描述材料的
动态力学行为。
表 1 材料物态变化与层裂类型
Table 1 Matter state variation and spallation classification

p H /GPa
Sn材料 u p /(km·s ) T H /K 物态 冲击熔化 分类
−1
本文 文献[35] 文献[42]
0.5 14.0 13.9 15.58 485.0 固态 未熔化 经典层裂
单晶 1.0 34.6 32.1 36.94 1 086.0 固液混合态 卸载熔化 微层裂

1.5 60.5 55.3 60.1 2 311.0 液态 加载熔化 微层裂
0.5 13.5 − − 484.0 固态 未熔化 经典层裂
纳米多晶 1.0 33.5 − − 1 062.0 固液混合态 卸载熔化 微层裂
1.5 61.0 − − 2 391.0 液态 加载熔化 微层裂

80

70 Experimental data [49]
MD data
[35]
60 MD data [42]
50 SC Sn
NC Sn
p H /GPa 40
30
20
10
0
−10
0 0.4 0.8 1.2 1.6 2.0
u p /(km·s )
−1
图 2 Hugoniot 压力 p H 与冲击速度 u p 的关系

Fig. 2 Relation of Hugoniot pressure p H and shock velocity u p
另外，通过计算得到了 Hugoniot 温度 T ，如表 1 所示。同时，通过对比 Sn 的压力-温度相图 [48,50-53] ，
H
判定了冲击过程中 Sn 的物态，这与 Liao 等 [39] 和 Wang 等 [42] 给出的冲击过程中 Sn 的物态一致。
2.2 应力波传播
图 3 表示不同冲击速度下加载过程中压力波（p ）形演化过程，其中黑色曲线为活塞加载结束时的
zz
波形，红色曲线表示应力波传播至自由面过程中的波形，蓝色曲线表示应力波即将到达自由面时的波
形。对于单晶 Sn 模型而言，当 u = 0.5 km/s 时，t = 10 ps 时的应力波波形为方波，其特点为波形的前沿和
p
尾巴陡峭，波形中间为 Hugoniot 平台，其压力表示 Hugoniot 压力；t = 20 ps 时，波形由方波开始变为梯形
波，主要原因是活塞移除后，加载端产生的稀疏波逐渐赶上压缩波，稀疏波与压缩波之间的相互作用导
致压缩波尾巴拖长，形成梯形波；t = 35 ps 时，稀疏波继续影响压缩波，Hugoniot 平台变窄，压缩波尾巴进
一步拖长，呈现出更加明显的梯形波。当 u = 1.0 和 1.5 km/s 时，单晶 Sn 的波形演化过程基本一致，且应
p
力波均以梯形波的形式抵达自由面。
对于纳米多晶 Sn 模型，当 u = 0.5 km/s 时，t = 10 ps 时的应力波前沿不如单晶 Sn 的波形陡峭，波前
p
沿呈现一定宽度，Hugoniot 平台宽度也相对较小，这可能与晶界和原子结构等因素有关。冲击过程中，冲

023101-4