Page 72 - 《软件学报》2020年第12期

3738 Journal of Software 软件学报 Vol.31, No.12, December 2020

Fig.1 Feature coding function
图 1 特征编码函数

2.2 新的适应度函数及适应度塑造方法
在计算样本适应度时,传统的适应度函数具有潜在的局限性.一般而言,大多数算法中对于样本的评估都是
基于测试集的分类准确率的,也就是说,每一次更新都会选取表现最好的一些特征序列,因此就会忽略维度缩减
的重要性.但是有时候在处理一些高维数据的时候,能够选择更少的特征也是具有实际应用价值的,所以本文就
传统适应度函数的弊端提出了一个新的适应度函数,将特征缩减也加入特征选取的考虑范围.
新的适应度函数如公式(10)所示:
f ⎧ ()x = i ρ CA + (1 ρ ⋅ − ) DR⋅
⎪
⎪
⎨ 90.99+ ⎛ ⎜ ϕ ⎞ ⎟ (10)
⎪ ρ = ⎝ 100 ⎠
⎪ 10
⎩
ϕ表示数据特征维数;关于参数ρ的取值与数据特征个数相关,其函数图像由图 2 给出;式中 CA 和 DR 为分
类准确率和维度缩减率(CA 和 DR 的定义在第 3.1 中进行详细说明).

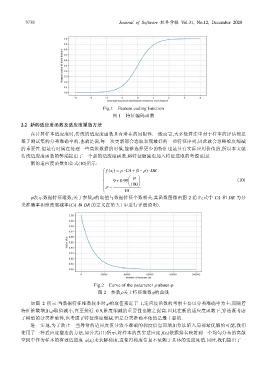
Fig.2 Curve of the parameter ρ about ϕ
图 2 参数ρ关于特征维数ϕ的曲线

如图 2 所示:当数据特征维数较小时,ρ的取值接近于 1,适应度函数的考察主要以分类准确率为主;而随着
特征维数增加,ρ取值减小,直至接近 0.9,维度缩减的重要性也随之提高.因此在新的适应度函数下,算法既考虑
了模型的分类准确性,也考虑了特征维度缩减,但是分类准确率依然是最主要的.
进一步地,为了防止一些异常的适应度值导致不准确的梯度信息而增加算法陷入局部最优解的可能,我们
使用了一种适应度塑造的方法,如公式(11)所示,将样本的真实适应度 f(x i )依据排名映射到一个均匀分布的离散
空间中作为样本的有效适应度 u(x i )来求解梯度,这使得梯度信息不依赖于具体的适应度值.同时,我们提出了一