Page 228 - 《软件学报》2020年第12期

3894 Journal of Software 软件学报 Vol.31, No.12, December 2020

第1阶段:插入 布鲁姆过滤器 第2阶段:匹配
掩码:/18 1 r
3 H 1(b 1)
H 1(P AS1)
2 H 2(b 1)
H 2(P AS1) 0 b 1=198.3.13.28/18
... ... ...
H k(P AS1) 1 H k(b 1)
2
/21 ...
...
0 r
自治域前缀全集
P AS3=198.1.3.0/24 H 1(a 1) 0 1 H 1(b 2)
P AS4=198.1.128.0/25 H 2(b 2)
H 2(a 1) 1 b 2=198.3.13.28/21 到达包目的地址
联盟成员前缀集 ... ... ... 198.3.13.28
P AS1=198.3.0.0/18 H k(a 1) H k(b 2)
P AS6=198.1.1.0/24 1
...
0
/24 ...
...
3 a
H 1(P AS6) 1 H 1(b 3)
0
H 2(P AS6) 0 H 2(b 3) b 3=198.3.13.28/24
... ...
...
H k(P AS6) H k(b 3)
3
1
第1阶段:插入 布鲁姆过滤器 第2阶段:匹配
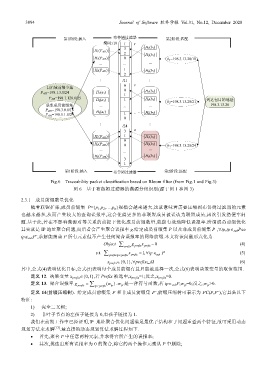
Fig.6 Traceability packet classification based on Bloom filter (from Fig.1 and Fig.3)
图 6 基于布鲁姆过滤器的溯源分组识别(源于图 1 和图 3)

2.3.1 成员前缀数量优化
随着联盟扩张,成员前缀集 P={p 1 ,p 2 ,…,p n }规模会越来越大,这就意味着需要压缩到布鲁姆过滤器的元素
也越来越多,从而产生较大的查询误报率,这会使得更多的非联盟成员被误认为联盟成员,再次引发搭便车问
题.基于此,若在不影响溯源对等关系的前提下优化成员前缀数量,就能有效地降低误报率.所谓成员前缀优化
−
其实就是 IP 地址聚合问题,而后者会产生聚合误报率 g.给定成员前缀集 P 以及非成员前缀集 P ,∀ip,ip∈ sub P⇔
−
ip∉ sub P ,求解能覆盖 P 所有元素但不产生任何聚合误报率的网络前缀.本文将该问题形式化为
Object ∑ g x = 0 (4)
prefix prefix prefix
1, ip ∈
s.t. ∑ x =∀ P (5)
∈
prefix :ip prefix prefix sub
x prefix ∈{0,1},∀prefix⊆Ω (6)
其中,公式(4)表明优化目标,公式(5)表明每个成员前缀有且只能被选择一次,公式(6)表明决策变量的取值范围.
定义 12. 决策变量 x prefix ∈{0,1},若 Prefix 被选中,x prefix =1;反之,x prefix =0.
=
定义 13. 聚合误报率 g prefix ∑ ip prefix (w ip ) .w ip 是一种符号函数,若 ip∈ sub P,w ip =0;反之,w ip >0.
∈
−
−
定义 14(前缀压缩树). 给定成员前缀集 P 和非成员前缀集 P ,前缀压缩树可表示为 PC(P,P ),它具备以下
特征:
1) 完全二叉树;
2) 非叶子节点的左孩子链接为 0,右孩子链接为 1.
我们在前期工作中已经证明,IP 地址聚合优化问题满足最优子结构和子问题重叠两个特征,故可采用动态
规划方法来求解 [13] .最直接的动态规划算法求解过程如下.
• 首先,聚合 P 中任意两种元素,并求得它所产生的误报率;
• 其次,挑选出所有误报率为 0 的聚合,将它的两个操作元素从 P 中删除;