Page 225 - 《软件学报》2020年第12期

鲁宁 等:联盟模式下高效单包溯源方法研究 3891

域间攻击路径回溯过程:受害者 V 1 携带攻击样本包 p 向 AS 6 的控制服务器发起溯源请求,该服务器收到请
求后,依据第 2.2.1 节的域内攻击路径回溯过程,能够准确识别出边界路由器 R 5 以及攻击包的入标签β和密钥
SK .基于此,即可判定此次攻击来自域外,随后向联盟注册服务器发起认证请求.该服务器收到请求后,首先利
AS 1
用攻击包源地址判定攻击域位置.如果该源地址不属于任何成员域,那么此次攻击就来自非成员域(就成员域来
说,它的所有域外匿名流都已被清理,只剩域内匿名流可能会流入受害域),溯源任务结束;反之,则可能来自成员
域,但需要进一步证实.为此,查询密钥与成员前缀的映射表,证实 SK AS 1 就是成员域 AS 1 的唯一密钥.随后,携带入
标签β向 AS 1 的控制服务器发起域内溯源请求.该服务器通过查询 AS 1 各边界路由器的 BGP 路由表,即可推测出
AS 1 到 AS 6 的路由路径,进而确定边界路由器 R 5 .然后,再执行第 2.2.1 节域内回溯过程,找到入口 R 1 和 R 2 .

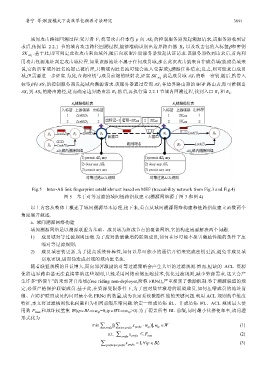
Fig.5 Inter-AS link fingerprint establishment based on MEF (traceability network from Fig.3 and Fig.4)
图 5 基于对等过滤的域间链路指纹建立(溯源网络源于图 3 和图 4)

以上内容从整体上概述了域间溯源基本原理,接下来,重点从域间溯源网络构建和链路指纹建立函数两个
角度展开叙述.
a. 域间溯源网络构建
域间溯源网络是以溯源联盟为基础、成员域为组成节点的覆盖网络,它的构建需要解决两个问题.
1) 成员域对等过滤规则压缩.为了应对数量激增的联盟成员,如何在尽可能不损害激励性能的条件下压
缩对等过滤规则;
2) 成员域密钥更新.为了提高系统鲁棒性,如何以尽可能小的通信开销来完成密钥更新,避免非成员域
窃取密钥,进而伪造成员域的域内匿名流.
随着联盟规模的日益增大,面向部署激励的对等过滤策略会产生大量的过滤规则.然而,短缺的 ACL 资源
使得边界路由器无法直接容纳这些规则,只能采用网络前缀压缩技术,优化过滤规则,减少资源需求.这又会产
生许多“搭便车”的未部署自治域(free riding non-deployer,简称 FRNd),严重损害了激励机制.鉴于溯源联盟的规
定,必须严格保护联盟成员.基于此,在资源受限条件下,为了应对数量激增的联盟成员,如何压缩成员的地址前
缀、在防护联盟成员的同时最小化 FRNd 的数量,成为决定系统激励性能的关键问题.利用 ACL 规则的单维度
特征,本文将过滤规则优化问题归为相同前缀压缩问题.给定一组成员集 BL、非成员集 WL、ACL 规则最大使
用数 F max 和地址权重集 W(ip∈BL⇒w ip =0;ip∈WL⇒w ip >0).为了覆盖所有 BL 前缀,同时最小化搭便车率,该问题
形式化为
min ∑ [(∑ x ⋅ w )],w ∈ W (1)
∈
prefix ip prefix prefix ip ip
s.t. ∑ x ≤ F (2)
prefix prefix max
1, ip ∈
∑ prefix :ip prefix x prefix =∀ BL (3)
∈