Page 43 - 《软件学报》2020年第11期

王占占 等:基于择优协作策略的 PES 算法在整数规划问题上的应用 3359

3500
最佳值
平均值
3000
2500
2000
1500
1000
500
0 200 400 600 800 1000
迭代次数
P 6 P 7 P 8
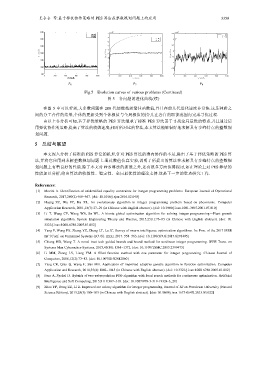
Fig.5 Evolution curves of various problems (Continued)
图 5 各问题的进化曲线(续)
在图 5 中可以看到,大多数问题在 200 代便能找到最佳函数值,并且在前几代进化速度非常快.这是种群之
间的分工合作的结果,个体的更新受到个体极值与全局极值的指引,在各自的职能范围内完成寻优过程.
由以上各分析可知,基于择优策略的 PES 算法继承了标准 PES 算法善于寻找全局最优的特点,并且通过运
用择优协作的策略,提高了算法的收敛速度;相对所对比的算法,本文算法能够很好地求解具有多峰特点的整数规
划问题.

5 总结与展望

本文深入分析了标准的 PES 算法的机理,针对 PES 算法的群内协作的不足,提出了基于择优策略的 PES 算
法,并将它应用到求解整数规划问题上.通过数值仿真实验,说明了所提出的算法在求解具有多峰特点的整数规
划问题上有着良好的性能.除了本文对 PES 算法的拓展之外,还有很多方面值得探讨,如在理论上对 PES 算法的
性能加以分析;给出算法的收敛性、稳定性、全局最优性的理论支持.这是下一步的重点研究工作.

References:
[1] Moeini A. Identification of unidentified equality constraints for integer programming problems. European Journal of Operational
Research, 2017,260(2):460−467. [doi: 10.1016/j.ejor.2016.12.040]
[2] Huang ZC, Wu FC, Hu XL. An evolutionary algorithm to integer programming problem based on pheromone. Computer
Application Research, 2001,18(7):27−29 (in Chinese with English abstract). [doi: 10.3969/j.issn.1001-3695.2001.07.010]
[3] Li T, Wang CF, Wang WB, Su WL. A bionic global optimization algorithm for solving integer programming—Plant growth
simulation algorithm. System Engineering Theory and Practice, 2015,25(1):76−85 (in Chinese with English abstract). [doi: 10.
3321/j.issn:1000-6788.2005.01.012]
[4] Yang F, Wang PX, Zhang YZ, Zheng LT, Lu JC. Survey of swarm intelligence optimization algorithms. In: Proc. of the 2017 IEEE
Int’l Conf. on Unmanned Systems (ICUS). IEEE, 2017. 558−563. [doi: 10.1109/ICUS.2017.8278405]
[5] Chiang HD, Wang T. A novel trust-tech guided branch-and-bound method for nonlinear integer programming. IEEE Trans. on
Systems Man Cybernetics-Systems, 2015,45(10):1361−1372. [doi: 10.1109/TSMC.2015.2399475]
[6] Li MM, Zhang LS, Liang YM. A filled function method with one parameter for integer programming. Chinese Journal of
Computers, 2008,12(2):73−83. [doi: 10.1007/BF02842060]
[7] Yang CR, Qian Q, Wang F, Sun MH. Application of improved adaptive genetic algorithm in function optimization. Computer
Application and Research, 2018,35(4):1042−1045 (in Chinese with English abstract). [doi: 10.3321/j.issn:1000-6788.2005.01.012]
[8] Bera A, Sychel D. Hybrids of two-subpopulation PSO algorithm with local search methods for continuous optimization. Artificial
Intelligence and Soft Computing, 2015,9119:307−318. [doi: 10.1007/978-3-319-19324-3_28]
[9] Zhao YP, Dong ZZ, Li Z. Improved ant colony algorithm for integer programming. Journal of Xi’an Petroleum University (Natural
Science Edition), 2013,28(3):100−103 (in Chinese with English abstract). [doi: 10.3969/j.issn.1673-064X.2013.03.022]