Page 137 - 《水产学报》2025年第8期

张铮，等 水产学报, 2025, 49(8): 089512

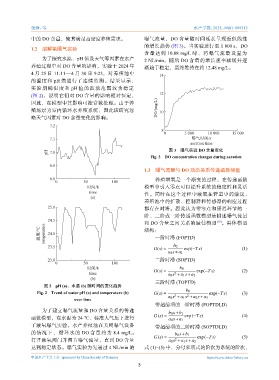
中的 DO 含量，使其满足高密度养殖需求。 曝气流量，DO 含量随时间延长呈现近似线性

的增长趋势 (图 3)。当实验进行至 1 800 s，DO
1.2 溶解氧曝气实验
含量达到 10.88 mg/L 时，将曝气流量设置为
为了探究水温、pH 值及天气等因素在水产 2 NL/min，随后 DO 含量的增长速率减缓并逐
养殖过程中对 DO 含量的影响，实验于 2024 年 渐趋于稳定，最终维持在约 12.48 mg/L。
4 月 25 日 11:11—4 月 30 日 9:23，对养殖池中 14
的温度和 pH 值进行了连续监测。结果显示，
实验期间温度和 pH 值的波动范围较为稳定
(图 2)，说明它们对 DO 含量的影响相对恒定， 12
因此，在模型中其影响可按常数处理。由于养
殖场景为室内循环水养殖系统，因此该研究忽 DO/(mg/L) 10
略天气因素对 DO 含量变化的影响。

7.2
8
0 5 000 10 000 15 000
7.1 曝气时间/s
aeration time
pH 7.0 图 3 曝气实验 DO 含量变化
Fig. 3 DO concentration changes during aeration

6.9
1.3 曝气流量与 DO 动态关系传递函数模型
6.8 养殖增氧是一个渐变的过程，在传递函数
0 50 100
时间/h 模型中引入零点可以提升系统的稳定性和灵活
time 性。同时在这个过程中液氧在管道中的输送、
(a)
养殖池中的扩散、控制器和传感器的响应过程
25.0 都存在时滞。因此认为带零点和延迟环节的一
阶、二阶或三阶传递函数模型是描述曝气流量
24.5 和 DO 含量之间关系的最佳模型 [10] 。具体模型
温度/°C temperature 24.0 结构： (FOPTD)
一阶时滞

23.5 G(s) = b 0 exp(−T s) (1)
a 0 s+a 1
23.0 二阶时滞 (SOPTD)
0 50 100
时间/h b 0
G(s) = exp(−T s) (2)
time a 0 s +a 1 s+a 2
2
(b) 三阶时滞 (TOPTD)
图 2 pH (a)、水温 (b) 随时间的变化趋势
b 0
Fig. 2 Trend of water pH (a) and temperature (b) G(s) = exp(−T s) (3)
3 2
a 0 s +a 1 s +a 2 s+a 3
over time
带超前项的一阶时滞 (FOPTDLD)
为了建立曝气流量和 DO 含量关系的传递
b 0 s+b 1
函数模型，在水温为 24 ℃、标准大气压下进行 G(s) = a 0 s+a 1 exp(−T s) (4)
了液氧曝气实验。水产养殖池在关闭曝气设备 带超前项的二阶时滞 (SOPTDLD)
的情况下，循环水的 DO 含量约为 8.4 mg/L。 b 0 s+b 1
G(s) = exp(−T s) (5)
打开液氧阀门并调节曝气流量，直到 DO 含量 a 0 s +a 1 s+a 2
2
达到稳定状态。曝气实验为先通过 4 NL/min 的 式 (1)~(5) 中，分母多项式的阶次为系统的阶次，

中国水产学会主办 sponsored by China Society of Fisheries https://www.china-fishery.cn
3