Page 406 - 《软件学报》2026年第1期

曹金政 等: 格上困难问题量子求解算法综述 403

第 3 阶段, 随着量子算法的发展, 研究者开始探索多种途径设计量子筛法. 2021 年, Chailloux 等人 [54] 将 k-结构
问题进一步分解, 将其转化为碰撞搜索问题, 进而使用基于量子漫步的碰撞搜索算法给出了新的量子筛法复杂度.
Bonnetain 等人 [55] 进一步提出了量子多碰撞搜索技术, 通过一次量子漫步同时求出多个碰撞. 该阶段量子筛法的加
速原理已不局限于 Grover 量子搜索, 而开始探索更多样化的量子算法设计方式.

[48]
Becker 等人 , 2016 Laarhoven 等人 , 2013
[51]
BDGL 筛法等优化算法 基于Grover 量子搜索的筛法
[54]
Chailloux 等人 , 2021 Wang 等人 , 2021 Kim 等 , 2021 Herold 等人 , 2018
[76]
[73]
[72]
筛法结合量子碰撞 量子2筛法 量子NV 筛法线路设计 量子元组筛法新结构
[60]
Chailloux 等人 , 2023 Bonnetain等人 , 2023 Albrecht 等人 , 2023
[55]
[56]
量子3、4筛法 量子多碰撞筛法 多种量子筛法分析
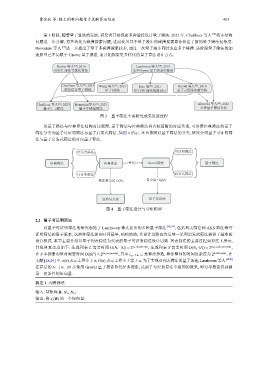
图 3 量子筛法主要研究成果发展过程

从量子筛法与经典算法结构对比观察, 量子筛法与经典筛法具有较清晰的对应关系, 可参照经典筛法将量子
筛法分类为量子可证明筛法与量子启发式筛法, 如图 4 所示. 本节按照对量子筛法的分类, 依次介绍量子可证明筛
法与量子启发式筛法的对应量子算法.

启发式筛法 可证明筛法

经典筛法 经典搜索 替代 Grover搜索 量子筛法

可证明筛法 启发式筛法
￣
√
搜索复杂度 O(N) 复杂度 O( N )

经典复杂度 量子复杂度
图 4 量子筛法设计与分析模型

2.1 量子可证明筛法
对量子可证明筛法的研究起始于 Laarhoven 等人提出的多种量子筛法 [48,49] , 包括列表筛法和 AKS 筛法等可
证明筛法的量子版本, 这两种筛法提出时间最早, 结构简洁, 其设计思路也为后续一系列启发式筛法提供了基本的
设计模式. 本节主要介绍以量子列表筛法为代表的量子可证明筛法设计思路. 列表筛法的主要过程如算法 1 所示,
其经典复杂度如下: 生成列表 L 需要时间 O(N 1 ·|L|) = 2 (c g +2c t )n+o(n) , 生成列表 S 需要时间 O(N 2 ·|L|) = 2 (c g +c b /2+c t )n+o(n) ,
在 S 中搜索向量对需要时间 O(|S | ) = 2 (2c g +c b )n+o(n) , 其中 c g , c b , c t 是算法参数, 算法整体的时间复杂度为 2 2.465n+o(n) . 在
2
文献 [48,49] 中, o(n) 表示上界小于 n, O(n) 表示上界小于等于 n. 为了实现对列表筛法的量子加速, Laarhoven 等人 [48,49]
在算法的 6、14、19 步使用 Grover 量子搜索替代经典搜索, 达到了与经典算法中相同的效果, 即穷举搜索得到满
足一定条件的短向量.

算法 1. 列表筛法.

输入: 基矩阵 B, N 1 , N 2 ;
L(B) 的一个短向量.
输出: 格