Page 152 - 《软件学报》2025年第10期

程石 等: 基于两种新标量表示的安全高效标量乘算法 4549

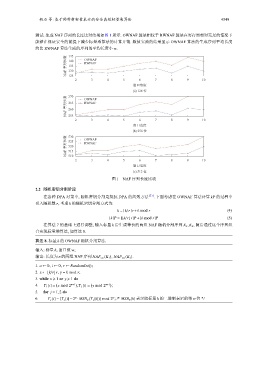
测试. 生成 NAF 序列的长度比对结果如图 1 所示. OWNAF 算法相较于 RWNAF 算法在寄存器相对充足的情况下
能够在保证安全的前提下减少标量乘算法的计算开销. 数值实验的结果显示 OWNAF 算法的生成序列平均长度
约比 RWNAF 算法生成的序列的平均长度小 w.
145 OWNAF
NAF 序列长度 140 RWNAF

135
130
125
2 3 4 5 6 7 8 9 10
窗口宽度
(a) 128 位
270
NAF 序列长度 265 OWNAF
RWNAF
260
255
2 3 4 5 6 7 8 9 10
窗口宽度
(b) 256 位
530
NAF 序列长度 525 OWNAF
RWNAF
520
515
510
2 3 4 5 6 7 8 9 10
窗口宽度
(c) 512 位
图 1 NAF 序列长度比较

2.2 随机密钥分割阶段
在各种 DPA 对策中, 随机密钥分割是抵抗 DPA 的高效方法 [21] . 下面考虑在 OWNAF 算法计算 kP 的过程中
引入随机数 r, 考虑 k 的随机密钥分割方式为:

k = ⌊k/r⌋r +k mod r (4)

[k]P = [⌊k/r⌋r]P+[k mod r]P (5)
在算法 7 的基础上进行调整, 输入标量 k 后生成等长的两组 NAF 随机分割序列 K 1 ,K 2 , 随后通过这个序列组
合实现标量乘算法, 如算法 8.
算法 8. 标量 k 的 OWNAF 随机分割算法.

输入: 标量 k, 窗口值 w;
n 的两组 NAF NAF ow (K 1 ) NAF ow (K 2 ).
,
输出: 长度为 序列
,
1. a ← 0 i ← 0 r ← RandomInt();
,
2. x ← ⌊k/r⌋r y = k mod r;
,
3. while x ⩾ 1 or y ⩾ 1 do
( ) ( )
4. T 1 [i] = x mod 2 w+1 ; T 2 [i] = y mod 2 w+1 ;
5. for j = 1,2 do
( ( ))
w
w
6. T j [i] = T j [i]−2 ·MSB w T j [i] mod 2 ; /* MSB w (k) 表示取标量 k 的二进制表示的第 w 位 */