Page 117 - 《软件学报》2025年第10期

4514 软件学报 2025 年第 36 卷第 10 期

期时间较短, 难度调整更加敏捷, 推荐用于快速进行难度调整的区块链和测试使用. 第 2 组参数周期出块数为 2 016,
每个块的目标出块为 5 min, 相对周期较长, 与目前常见的应用 PoW 共识机制的公链参数类似, 推荐应用于更为成
熟的公链应用.

表 1 难度调整算法参数表

参数 目标周期出块数 φ 父链出块目标比例 α 因子上界 µ 因子下界 ξ 加权系数 β 加权系数 γ
1 720 10 3 0.33 0.4 0.6
2 2 016 10 3 0.33 0.5 0.5
参数 目标时间 ET (min) 出块记录周期 ω 底数 δ 底数 δ A 父链A出块数边界 A low limit 父链B出块数边界 B low limit
1 1 440 4 10 1.2 320 5
2 10 080 3 10 1.2 1 516 6

2.4 应用基于素阶数域的后量子数字签名算法
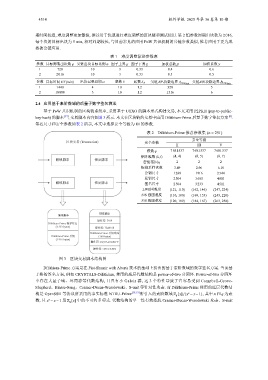
基于 PoW 共识机制的区块链系统中, 采用基于 UTXO 的脚本形式构建交易, 本文采用 P2PKH (pay-to-public-
key-hash) 的脚本 [17] , 交易脚本内容如图 3 所示. 本文在区块链的交易中应用 Dilithium-Prime 后量子数字签名方案 [2] .
签名尺寸和安全参数如表 2 所示, 本文中选择安全等级为 III 的参数.

表 2 Dilithium-Prime 推荐参数集 ( n = 251)

安全等级
区块交易 (Transaction) 安全参数
II III V
模数 q 7 681 537 7 681 537 7 681 537
矩阵维数 (k,l) (4, 4) (6, 5) (8, 7)
解锁脚本 锁定脚本
密钥范围 η 2 2 2
拒绝采样次数 3.49 2.96 6.10
公钥尺寸 1 288 1916 2 544
私钥尺寸 2 504 3 605 4 801
解锁脚本 锁定脚本 签名尺寸 2 504 3 233 4 511
LWE困难度 (121, 110) (162, 146) (247, 224)
SIS 强困难度 (110, 100) (169, 153) (243, 220)
SIS 弱困难度 (120, 109) (184, 167) (263, 238)

锁定脚本
解锁脚本
操作符: DUP
Dilithium-Prime 数字签名
(3 233 bytes)
操作符: Hash160
Dilithium-Prime 公钥哈希
Dilithium-Prime 公钥 (160 bytes)
(1 916 bytes)
操作符: EQUALVERIFY
操作符: CHECKSIG
图 3 区块交易脚本结构图

Dilithium-Prime 方案是在 Fiat-Shamir with Aborts 技术的基础上提出的基于素阶数域的数字签名方案. 当前基
于格的签名方案, 例如 CRYSTALS-Dilithium, 使用的底层代数结构是 power-of-two 分圆环. Power-of-two 分圆环
中存在大量子域、环同态等代数结构, 且具有小 Galois 群, 这 3 个特性导致了它容易受到 Campbell-Grove-
Shepherd、Biasse-Song、Cramer-Ducas-Wesolowski、S-unit 等针对性攻击. 而 Dilithium-Prime 使用的底层代数结
构是 OpenSSH 等协议所采用的事实标准 NTRU-Prime [18,19] 所引入的素阶数域 Z q [x]/(x − x−1), 其中 n 和 q 为素
n
n Z q [x] 中的不可约多项式. 代数结构的单一性有效抵抗 Cramer-Ducas-Wesolowski 攻击、S-unit
数, 且 x − x−1 是