Page 15 - 《软件学报》2025年第9期

3926 软件学报 2025 年第 36 卷第 9 期

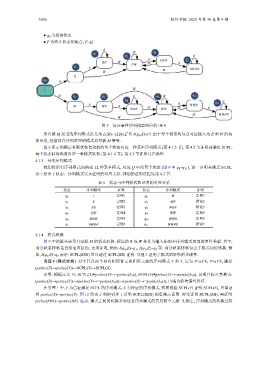
● q 0 为初始状态.
● F 为终止状态的集合, F=Q.

R
W q 4
q 2
q 3 R
R RWR q 5
RR W W R
RW
R RWRR
q 1
W
W
R
q 0
R
ε W
W q 6 q 7 R q 9 W q 10
q 8 R
R R WWR q 11
W WR R W W
WRR WW R
W WWRR
W
图 9 访存事件序列构造对应的 DFA

所有被 M 接受的序列模式定义为 L(M)={X|X∈Σ 且 * δ(q 0 ,X)∈F}.由于每个状态均包含对应输入为 R 和 W 的两
条出边, 任意访存序列对应的模式均可被 M 接受.
图 9 所示的确定有限状态自动机的每个状态对应一种基本序列模式 (第 4.1.3 节), 第 4.2 节证明其满足 SCPL;
每个状态转移函数对应一种模式转换 (第 4.1.4 节), 第 4.3 节证明其正确性.

4.1.3 基本序列模式
我们将所有序列模式归纳成 12 种基本模式, 对应 Q 中的每个状态 (图 9 中 q 0 –q 11 ), 逐一证明其满足 SCPL.
表 1 给出了状态、序列模式以及证明的对应关系. 详细的证明过程见第 4.2 节.

表 1 状态与序列模式和证明的对应关系

状态 序列模式 证明 状态 序列模式 证明
ε 定理1 W 定理7
q 0 q 6
q 1 R 定理2 q 7 WR 推论2
RR 定理3 WRR 推论3
q 2 q 8
RW 定理4 WW 定理8
q 3 q 9
q 4 RWR 定理5 q 10 WWR 定理9
RWRR 定理6 WWRR 推论5
q 5 q 11

4.1.4 模式转换
图 9 中的箭头表示自动机 M 的状态转移, 标注的 R 或 W 是作为输入添加至序列模式尾部的事件类型. 其中,
部分状态转移是自然而直接的, 无须证明, 例如 δ(q 0 ,R)=q 1 , δ(q 7 ,R)=q 8 等. 部分状态转移包含了模式间的转换. 例
如, δ(q 2 ,R)=q 2 表示: SCPL(RRR) 可以通过 SCPL(RR) 证明. 引理 1 证明了模式间转换的正确性.
引理 1 (模式转换). 对于任意两个具有相同首元素和尾元素的序列模式 X 和 Y, 记为 X=aX′b, Y=aY′b, 满足
(perloc(X)→perloc(Y))→SCPL(Y)→SCPL(X).
证明: 根据定义 19, SCPL(X)≜perloc(X)→¬perloc(b,a), SCPL(Y)≜perloc(Y)→¬perloc(b,a), 证明目标可替换为:
(perloc(X)→perloc(Y))→(perloc(Y)→¬perloc(b,a))→(perloc(X)→¬perloc(b,a)), 由蕴含的传递性得证.
在引理 1 中, Y 为已证满足 SCPL 的序列模式, X 为待证的序列模式, 想要根据 SCPL(Y) 证明 SCPL(X), 只需证
明 perloc(X)→perloc(Y). 图 10 给出了利用引理 1 证明 SCPL(RRR) 的思路示意图. 即先证明 SCPL(RR), 再证明
perloc(RRR)→perloc(RR). 注意, 模式之间的转换必须包含序列模式的首尾两个元素. 实际上, 序列模式的转换过程