Page 19 - 《软件学报》2025年第5期

杨紫萱 等: 基于 PAC 学习的组合式概率障碍证书生成 1919

相比之下, PACBC-DM 在将非线性不等式线性化时采用基于微分中值定理的区间线性化方法, 其余方面与
PACBC 相同. 此外, CPBC 采用基于大 M 法的混合整数规划方法来求解障碍证书, 并使用基于微分中值定理的区
间线性化方法处理非线性约束条件. 对于一些复杂的动力系统, 本文通过求解 1 组组合式的 PAC 障碍证书, 以验
证其概率安全性.
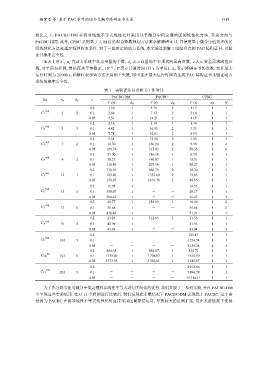
如表 1 所示, n x 为动力系统中状态变量的个数, d f 表示向量场中多项式的最高次数, ε 表示安全需求阈值参

数, 对于所有样例, 置信度水平参数 β = 10 −12 . T 表示计算时间 (以 s 为单位), d B 表示障碍证书的次数. 允许最大
运行时间为 20 000 s, 画横杠表示该方法在用例上失败, 即不能在最大运行时间内生成 PAC 障碍证书来验证动力
系统的概率安全性.

表 1 实验评估以及相关工作对比

PACBC-DM PACBC CPBC
Ex n x d f ε
T (s) d B T (s) d B T (s) d B N
0.2 1.50 1 3.71 2 1.17 1 1
[39]
C 1 2 2 0.1 2.89 1 7.13 2 2.14 1 1
0.05 5.51 1 14.21 2 4.17 1 1
0.2 2.16 1 2.19 1 1.79 1 1
[38]
C 2 3 3 0.1 4.02 1 16.35 2 3.33 1 1
0.05 7.78 1 32.63 2 6.54 1 1
0.2 5.54 1 75.54 2 5.05 1 3
[40]
C 3 7 2 0.1 14.30 1 166.14 2 9.58 1 4
0.05 120.74 1 315.03 2 20.33 1 6
0.2 23.00 1 186.58 1 6.74 1 1
[40]
C 4 9 2 0.1 30.27 1 190.07 1 13.31 1 1
0.05 116.40 1 207.56 1 26.27 1 1
0.2 118.93 1 668.79 2 10.30 1 1
[41]
C 5 12 1 0.1 129.20 1 1 333.60 2 19.85 1 1
0.05 150.67 1 2 639.76 2 40.05 1 1
0.2 15.74 1 － － 14.51 1 1
[38]
C 6 15 5 0.1 550.07 1 － － 28.17 1 1
0.05 588.67 1 － － 56.47 1 3
0.2 21.77 1 258.19 1 18.40 1 2
[38]
C 7 17 5 0.1 39.68 1 － － 35.64 1 2
0.05 418.40 1 － － 71.21 1 1
0.2 23.25 1 312.65 1 21.53 1 1
[38]
C 8 19 5 0.1 45.96 1 － － 41.93 1 1
0.05 93.95 1 － － 83.94 1 3
0.2 － － － － 789.11 1 1
[38]
C 9 101 5 0.1 － － － － 1 574.74 1 1
0.05 － － － － 3 136.34 1 1
0.2 884.38 1 864.17 1 824.72 1 1
[5]
C 10 101 5 0.1 1 735.06 1 1 704.87 1 1 616.99 1 1
0.05 3 373.56 1 3 362.61 1 3 185.07 1 1
0.2 － － － － 4 012.86 1 1
[38]
201 5 0.1 7 894.78 1 1
C 11 － － － －
0.05 － － － － 15 714.11 1 1

为了充分展示使用微分中值定理对非线性不等式进行区间化的优势, 我们开展了一系列实验, 并在 PACBC-DM
中呈现这些实验结果. 在对 11 个样例进行比较后, 我们发现在多数情况下 PACBC-DM 表现优于 PACBC. 这主要
是因为 PACBC 在将非线性不等式线性化时直接采用区间乘法运算, 导致较大的区间扩张, 这在某些情况下使得