Page 247 - 《软件学报》2024年第4期

李贺 等: 基于顶点组重分配的动态增量图划分算法 1825

划分问题, 则无法保证图划分的质量, 前面我们已经详细分析了该问题. 因此, 在利用动态处理器处理完图的动态
变化后, 在涉及的分区中利用局部优化器进行局部优化, 从而获得高质量的划分结果.

P 1 P 2 P 1 P 2
d b f h
d a b
×
a

c e f
c e g

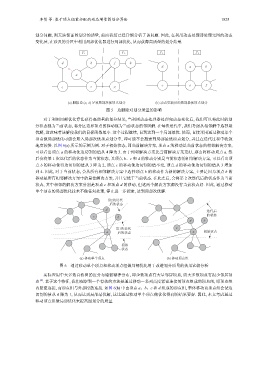
(a) 删除边 (a, d) 导致局部次优顶点划分 (b) 动态更新后的局部最优顶点划分
图 5 边删除对划分质量的影响

对于利用局部优化算法获得高质量的划分结果, 当利用动态处理器处理完动态变化后, 我们可以将此时的划
分状态视为当前状态, 将分区边界顶点的移动视为当前状态的邻居解. 在每次迭代中, 我们考虑从相邻解中选择最
优解, 这意味着该解使我们的目标函数最小. 这个过程继续, 直到达到一个局部最优. 然而, 直接采用通过移动单个
顶点做局部优化可能会陷入局部次优顶点划分中, 即可能不会搜索到局部最优顶点划分, 并且在迭代过程中收敛
速度较慢. 以图 6(a) 所示的示例为例. 对于初始状态, 即当前解决方案, 顶点 a 的移动是当前状态的相邻解决方案,
可以看出顶点 a 的移动使边切割的值从 4 降为 3. 由于相邻解决方案比当前解决方案更好, 那么将移动顶点 a. 然
后会将第 1 次迭代后的状态作为当前状态, 其顶点 b、c 和 d 的移动分别是当前状态的相邻解决方案, 可以看出顶
点 b 的移动使得边切割的值从 3 降为 2, 顶点 c 的移动使边切割的值不变, 顶点 d 的移动使边切割的值从 3 增加
到 4. 因此, 对于当前状态, 会从所有相邻解决方案中选择顶点 b 的移动作为新的解决方案, 主要是因为顶点 b 的
移动是所有相邻解决方案中的最佳解决方案, 并且它优于当前状态. 在此之后, 会将第 2 次迭代后的状态作为当前
状态, 其中相邻的解决方案分别是顶点 c 和顶点 d 的移动, 但这两个解决方案都没有当前状态好. 因此, 通过移动
单个顶点的局部优化技术不做任何处理, 停止进一步搜索, 达到局部次优解.

第2次迭代
后的状态
d 迭代后
的状态
c b
d b
第1次迭代 c
a 后的状态 a 初始状态

初始
状态

(a) 移动单个顶点 (b) 移动顶点组
图 6 通过移动单个顶点和移动顶点组做局部优化用于改进划分质量的效果比较分析

实际应用中大多数自然图的度分布遵循幂律分布, 即少数顶点有大量邻居顶点, 而大多数顶点有很少邻居顶
点 [4] . 基于这个特征, 我们观察到一个有效的方法是通过移动一系列高度紧密连接的顶点组成的顶点组, 即顶点组
内紧密连接, 而顶点组与外部松散连接. 如图 6(b) 中由顶点 a、b、c 和 d 组成的顶点组, 整体移动该顶点组会使边
切割的值从 4 降为 1, 从而达到局部最优解, 这比通过移动单个顶点做优化得到的结果要好. 因此, 本文考虑通过
移动顶点组做局部优化来提高图划分的质量.