Page 143 - 《软件学报》2024年第4期

闫涛 等: 一种分组并行的轻量化实时微观三维形貌重建方法 1721

2 GPLWS-Net: 基于分组并行的轻量化实时微观三维形貌重建方法

2.1 多聚焦图像序列的子域数据分组并行理论分析
基于多聚焦图像序列的微观三维形貌重建方法利用光学设备成像过程的有限景深判定聚焦区域与相机间
的相对距离, 进而还原待测场景的三维形貌. 根据高斯成像公式可得, 物距的倒数与像距的倒数之和等于焦
距的倒数:
1 1 1
= + (2)
f u v
其中, f 表示镜头焦距, u 表示物体到透镜的距离, v 表示成像到透镜的距离.
上述理论表明, 多聚焦图像三维形貌重建的本质是从一系列不同聚焦水平的图像序列中挖掘深度信息.
其中, 单帧图像中的聚焦与散焦变换可以通过全聚焦图像的滤波得到. 因此, 局部聚焦图像 I L 可以通过全聚
焦图像 I 与点扩散函数 h 的卷积得到:
I L =I*h (3)
其中, 点扩散函数在光学成像模式中可以简化成如下高斯函数:
2
1  i + j  2
hi exp −  (4)
( , ) j =

2 σ p h  2σ h 
其中, σ h 用来刻画一幅图像的模糊水平. 研究表明, 在 I i,j 位置的模糊水平σ h 与场景深度 u 存在如下关系 [32] :
κ f 2 | uu− |
σ ( , )ij = f (5)
h
A ( u u − ) f
f
2
其中, u f 为相机设置的聚焦位置, κ为相机参数, A 为相机焦距与透镜直径的比值. 假定 M=κf /A(u f −f), 对公式
(5)求导可得:
 u f
−
∂ σ ( , ) | uu |   u − 1, u < u f
ij
h = M f =  (6)
u ∂ u  u f
  1− u , u ≥ u f
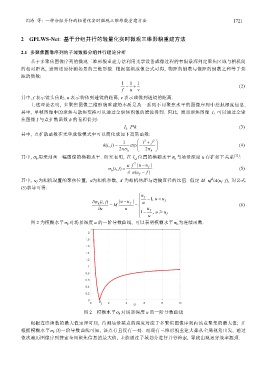
图 2 为模糊水平σ h 对场景深度 u 的一阶导数曲线, 可以表明模糊水平σ h 为连续函数.

图 2 模糊水平σ h 对场景深度 u 的一阶导数曲线

根据连续函数的最大值定理可知, 待测场景某点的深度对应于多聚焦图像序列内该点聚集的最大值; 并
根据模糊水平σ h 的一阶导数曲线可知, 该点有且仅有一处. 而现有三维形貌重建大都从全局视角出发, 通过
依次遍历图像序列搜索全局聚焦信息的最大值, 未能通过子域划分进行并行检索, 导致出现运行效率瓶颈.