Page 13 - 《软件学报》2021年第11期

武优西 等:无重叠条件严格模式匹配的高效求解算法 3339

12: for i=1 to 第 j 层结点数 step 1 do
13: 更新第 j 层第 i 个结点的最小、最大叶子;
14: end for
15: end for
16: return NetTree;
3.2.2 回溯算法
通过例 8 来说明采用回溯策略获得最左孩子路径的原理.
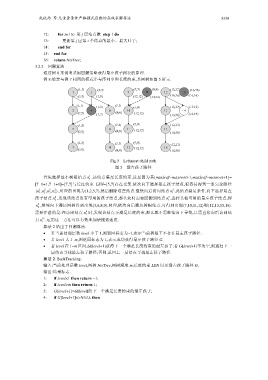
例 8:给定与例 7 相同的模式串与序列串和长度约束,其网树如图 5 所示.

Fig.5 Leftmost child path
图 5 最左孩子路径
1
首先选择最小树根结点 n ,该结点满足长度约束,这是因为其[minleaf−maxroot+1,maxleaf−minroot+1]=
1
[7−1+1,7−1+1]=[7,7]与长度约束 LEN=[5,7]存在交集.依次向下选择最左孩子结点,很容易得到一条完全路径
1
3
〈 nn 2 2 ,n n 〉 3 5 , 7 4 ,对应的出现为〈1,2,5,7〉,然后删除这些结点.继续向后访问结点 n ,此结点满足条件,向下选择最左
,
1
1
4
3
孩子结点 n ,发现该结点没有可用的孩子结点,那么此时需要回溯到结点 n ,选择其他可用的最左孩子结点,即
1
2
6
n ,继续向下遍历网树得到出现〈3,6,8,9〉.同理,依次向后遍历树根结点,可得到出现〈7,10,11,12〉和〈12,13,15,16〉.
2
9
需要注意的是:在访问结点 n 时,发现该结点不满足长度约束,那么就不需继续向下寻找,只需直接向后访问结
1
12
点 n .运用这一方法可以有效地加快搜索速度.
1
算法 2 给出了回溯算法.
• 若当前处理层数 level 小于 1,则返回标志为−1,表示当前树根下不存在最左孩子路径.
• 若 level 大于 m,则返回标志为 1,表示成功获得最左孩子路径 G.
• 若 level 在 1~m 区间,G[level+1]获得下一个满足长度约束的最左孩子:若 G[level+1]不为空,则递归下一
层结点寻找最左孩子路径;否则,返回上一层结点寻找最左孩子路径.
算法 2. BackTracking.
输入:当前处理层数 level,网树 NetTree,网树深度 m,长度约束 LEN 以及最左孩子路径 G.
输出:结果标志.
1: if level<1 then return −1;
2: if level>m then return 1;
3: G[level+1]=G[level]的下一个满足长度约束的最左孩子;
4: if G[level+1]<>NULL then