Page 119 - 《软件学报》2021年第10期

朱二周 等:一种采用新型聚类方法的最佳类簇数确定算法 3091

sd≥cd.所以,csd 函数的范围处于[0,1]之间,这样可以避免过度影响到 E(K)的极端情况.
*
*
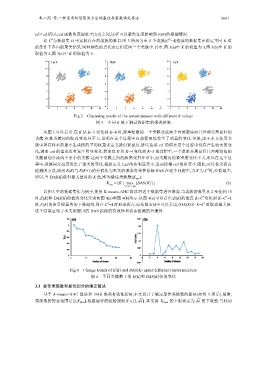
设 C 为数据集 D 中实际存在的类簇的数目.图 3 所示为由 4 个类簇(C =4)组成的数据集在给定不同 K 值
的条件下各自的聚类结果.同种颜色的点代表它们在同一个类簇中.其中,图 3(a)中 K 的取值为 3,图 3(b)中 K 的
取值为 4,图 3(c)中 K 的取值为 5.

Fig.3 Clustering results of the tested datasets with different K values
图 3 不同 K 值下测试数据集的聚类结果

从图 3 可以看出:在 K 从 K=3 变化到 K=4 时,原本松散的一个类簇变成两个内部紧凑而且外部分离良好的
类簇.但是类簇间的距离变化并不大,说明在这个过程中内部紧凑性发生了明显的变化.但是,由于本文使用类
簇中所有样本的最小生成树的平均权重来定义簇内紧密度,所以造成 cd 的值在这个过程中没有产生较大的变
化,进而 csd 的值也没有发生明显变化.然而在 K 从 K=4 变化到 K=5 的过程中,一个原本分离良好且内部紧凑的
类簇被划分成两个更小的类簇.这两个类簇之间的距离变得非常小,而类簇内的紧密度变化不大,所以在这个过
程中,类簇间分离度发生了很大的变化.根据定义 2,sd 的值明显变小,进而使得 csd 的值变小.因此,可以使用拐点
*
检测的方法,即用 E(K)与 E(K+1)的差值作为本文的聚类有效性指标 DAS.在这个问题中,当 K 为 C 时,差值最大,
所以,当 DAS(K)取得最大值时的 K 值,即为最佳类簇数(K opt ):
K  {| max {K DAS ( )}}K (6)
opt
K
2≤≤ n
以图 3 中的数据集作为例子,使用 K-means-AHC 算法对这个数据集进行聚类.当类簇的数量从 2 变化到 15
*
*
时,E(K)和 DAS(K)的值的变化分别如图 4(a)和图 4(b)所示.从图 4(a)可以看出:E(K)的值在 K=C 变化到 K=C +1
*
*
时,E(K)的值呈现显著的下降趋势,即在 C =4 时形成拐点.而从图 4(b)中可以看出,DAS(K)在 K=C 时取到最大值.
这个结果证明了本文所提出的 DAS 指标的有效性和拐点检测的合理性.

Fig.4 Change trends of E(K) and DAS(K) under different cluster numbers
图 4 不同类簇数下的 E(K)和 DAS(K)值的变化

3.3 最佳类簇数和最优划分的确定算法
基于 K-means-AHC 算法和 DAS 聚类有效性指标,本文设计了确定最佳类簇数的算法(如图 5 所示).通常,
类簇数的搜索范围是[2,K max ].根据通行的经验规则 K  [2, n ,本文将 K max 的上限设定为 n 的下取整.与此同
]