Page 73 - 《软件学报》2021年第9期

钱忠胜 等:面向关键字流图的相似程序间测试用例的重用 2697

1. 程序开始
public
2. 数组赋值 D1 原始数组
int
3. 数组循环
for
for
3.1. 判断
数值大小

是 3.2. 位置交换 if
否
null
4. 数组输出
null
D2 排序后数组

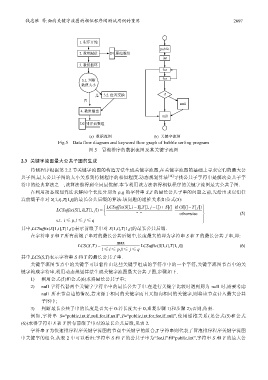
(a) 数据流图 (b) 关键字流图
Fig.5 Data flow diagram and keyword flow graph of bubble sorting program
图 5 冒泡排序的数据流图及其关键字流图
2.3 关键字流图最大公共子图的生成

待测程序根据第 2.2 节关键字流图的构造方法生成关键字流图,在关键字流图的基础上寻求它们的最大公
共子图,最大公共子图的大小关系到待测程序的相似程度.动态规划算法 [14] 寻找公共子字符串是解决公共子字
符串的经典算法之一,该算法能得到全局最优解.本节利用该方法求得相似程序的关键字流图最大公共子图.
在利用动态规划算法求解两个长度分别为 p,q 的字符串 S,T 的最长公共子串的问题之前,先给出求它们任
意前缀子串对 S[1,i],T[1,j]的最长公共后缀的算法.该问题的递推关系如公式(5):
[ ])⎫
⎧ LCSuf ( [1, −fix S i 1], [1, − j 1]) + T S [ ] if ( [ ] − i S i T j
LCSuffix S i T j ⎪
([1, ], [1, ]) = ⎨
⎩ " " otherwise ⎬ (5)
s.t. ≤ i ,1≤ p j ≤ q ⎪ ⎭
其中,LCSuffix(S[1,i],T[1,j])表示前缀子串对 S[1,i],T[1,j]的最长公共后缀.
在字符串 S 和 T 所有前缀子串对的最长公共后缀中,长度最大的即为字符串 S 和 T 的最长公共子串,即:
max
LCS (, )S T = LCSuffic ( [1, ], [1, ])S i T j (6)
i
j
1≤≤ p ,1≤ ≤ q
其中,LCS(S,T)表示字符串 S 和 T 的最长公共子串.
关键字流图节点中的关键字可以看作由这些关键字组成的字符串中的一个字符,关键字流图节点中的关
键字构成字符串,利用动态规划算法生成关键字流图最大公共子图,步骤如下.
1) 利用公式(5)和公式(6)求得最长公共子串;
2) null 字符代替两个关键字字符串中的最长公共子串.在进行关键字比较时遇到同为 null 时,需要考虑
null 所在节点边的情况,若来源于相同的关键字而且又指向相同的关键字,则将该节点计入最大公共
子图中;
3) 判断最长公共子串的长度是否大于 0:若长度大于 0,重复步骤 1)和步骤 2);否则,结束.
例如,字符串 S=“public,int,if,null,for,if,null”,T=“public,int,for,for,if,null”,使用递推关系(见公式(5)和公式
(6))求得字符串 S 和 T 所有前缀子串对的最长公共后缀,见表 2.

字符串 S 为快速排序程序关键字流图的节点中关键字的组合,T 字符串则代表了冒泡排序程序关键字流图
中关键字的组合.从表 2 中可以看出:字符串 S 和 T 的公共子串为“for,if”和“public,int”,字符串 S 和 T 的最大公