Page 7 - 《软件学报》2021年第9期
P. 7
王永平 等:取定 s 的严格 d-正则随机(3,2s)-SAT 问题的可满足临界 2631
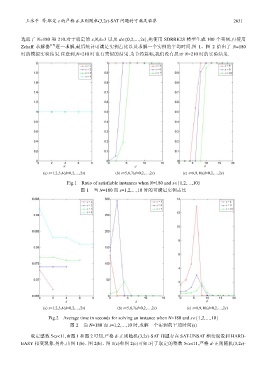
选取了 N=180 和 210.对于取定的 s,N,k=3 以及 d∈{0,2,…,2s},先使用 SDRRK2S 模型生成 100 个实例,再使用
Zchaff 求解器 [12] 逐一求解,最后统计可满足实例占比以及求解一个实例的平均时间.图 1、图 2 给出了 N=180
时的模拟实验结果.注意到,N=210 时也有类似的结果.为节约篇幅,我们没有展示 N=210 时的实验结果.
(a) s=1,2,3,4(d=0,2,…,2s) (b) s=5,6,7(d=0,2,…,2s) (c) s=8,9,10(d=0,2,…,2s)
Fig.1 Ratio of satisfiable instances when N=180 and s∈{1,2,…,10}
图 1 当 N=180 而 s=1,2,…,10 时的可满足实例占比
(a) s=1,2,3,4(d=0,2,…,2s) (b) s=5,6,7(d=0,2,…,2s) (c) s=8,9,10(d=0,2,…,2s)
Fig.2 Average time in seconds for solving an instance when N=180 and s∈{1,2,…,10}
图 2 当 N=180 而 s=1,2,…,10 时,求解一个实例的平均时间(s)
取定整数 5<s<11,由图 1 和图 2 可知,严格 d-正则随机(3,2s)-SAT 问题存在 SAT-UNSAT 相变现象和 HARD-
EASY 相变现象.另外,由图 1(b)、图 2(b)、图 1(c)和图 2(c)可知:对于取定的整数 5<s<11,严格 d-正则随机(3,2s)-