Page 220 - 《软件学报》2021年第9期

2844 Journal of Software 软件学报 Vol.32, No.9, September 2021

由于该方法计算复杂度较高,对于基于变元个数多于 4 的 S 盒设计的算法,求解效果不佳.图 4 表示经过算法 2
−2
后可求得的概率布尔多项式首项系数(单位:10 ).这里,首项统一视为 y 0 y 1 y 2 y 3 :
y = 0 x x x + 0 1 2 x x x + 0 1 3 x x + 0 1 x x + 0 2 x x + 0 3 x x + 1 2 x x + 2 3 1
y = 1 x x x + 013 x x + 01 x + 0 x x + 1 2 x + 1 x 3
y = 2 x xx + 0 1 2 x x x + 0 2 3 x x x + 1 2 3 xx + 1 3 x + 1 x x + 2 3 x + 2 1
y = x x x + 0 1 3 xx + 0 1 xx + 0 2 x + 0 x x x + 1 2 3 x x + 1 2 x + 1 x x + 2 3 1
3
12.9 15.0 1.4 11.6 9.3
9.8 17.7 1.4 10.4 10.1
10.2 12.7 1.6 15.4 9.5
12.7 14.7 1.4 14.4 10.3

Fig.4 Highest order coefficient of probability boolean polynomial
图 4 概率布尔多项式首项系数
再经过第 6 轮的非线性层 P64,由推论 1 可得到此 20 个比特位置平衡的概率(单位:%).

90.7 85.3 85.6 90.2 85.0
88.4 87.3 87.1 84.6 89.6
89.7 98.4 98.6 89.9 99.6
89.8 82.3 90.5 87.3 98.6

4
综上讨论,当(p 6 ,p 24 ,p 31 ,p 60 )遍历{0,1} 时,得到 6 轮加密后密文 20 个位置的平衡概率.证毕. □
4
60
为验证该 6 轮积分区分器的准确性,我们考虑布尔函数 y=f(k,m 1 ,m 2 ),当 m 1 遍历{0,1} 且 m 2 在{0,1} 中等
概率取值时,对固定的密钥 k 是否存在高概率零和区分器.根据定义,其相对于密钥 k 是 0 和区分器的概率是:
1 ⎧ ⎫
# m ∈
p = 60 ⎨ {0,1} : ⊕ f ( , k m m = , ) 0 . ⎬
60
k
2 ⎩ 2 m ∈ 4 1 2 ⎭
1 {0,1}
这样,就可以通过将 f 看作黑盒,对于 M 个随机选择的密钥 k:k 1 ,k 2 ,…,k M ,随机选定 N 个 m 2 : m (1) ,m (2) ,...,m ( )N ,
2 2 2
统计:
1
N
p =− ∑ 1 ⎣ ⎡ ⎢ m ∈ ⊕ 4 f ( , k m m 2 ⎥ () i ⎤ ) ,
,
1
i
1
i k
⎦
N
1 {0,1}
i=
并核实 p 1 k , p 2 k ,..., p k M 是否集中在一个聚集在 1 附近的小区域之内.
这样,就可通过简单的实验验证该结果(感谢金晨辉教授对本实验方法的指导).
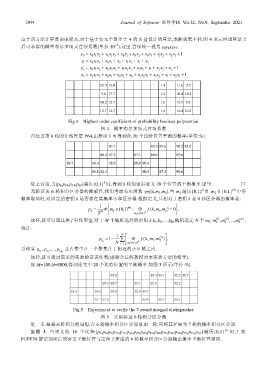
取 M=100,N=8000,得到论文中 20 个比特位置的平衡概率,如图 5 所示(单位:%).

Fig.5 Experiment to verify the 7-round integral distinguisher
图 5 实验验证 6 轮积分区分器
进一步,根据高阶积分的思想,在 6 轮概率积分区分器前加一轮,可将其扩展为 7 轮的概率积分区分器.
定理 3. 当明文的 16 个比特{p 5 ,p 8 ,p 9 ,p 10 ,p 11 ,p 26 ,p 27 ,p 28 ,p 29 ,p 30 ,p 35 ,p 42 ,p 50 ,p 51 ,p 61 ,p 63 }遍历{0,1} 16 时,7 轮
PUFFIN 算法加密后的密文平衡位置与定理 2 所述的 6 轮概率积分区分器输出概率平衡位置相同.