Page 89 - 《软件学报》2021年第8期

徐顺 等:面向异构计算的高性能计算算法与软件 2371

积分、构造 Fock 矩阵和求解广义特征值方程,兼具计算密集型和访存密集型的特点.计算双电子积分一般采用
解析的方法,是计算密集型的,计算量与体系大小的 4 次方成正比.在引入了 prescreening 方法后,可以有效降低
积分计算的 scaling,同时利用分子划片的方法,可以得到近似线性的 scaling 结果.构造 Fock 矩阵是访存密集型
的,有大量的随机不连续访存.如何协调处理计算积分和构造矩阵是异构优化自洽场计算的难点.2008
年,Yasuda [28] 首先提出利用 GPU 计算双电子积分.同年利用积分公式自动展开的方法将积分的计算转化为适合
GPU 运行的方式,取得了较好的结果.后来,Ufimtsev 等人 [29,30] 提出了预先排序的方法,实现了在 GPU 上构造
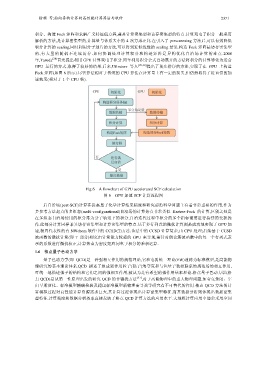
Fock 矩阵(如图 6 所示).尽管算法相对于传统的 CPU 算法在计算量上有一定的损失,但仍然取得了近百倍的加
速效果(相对于 1 个 CPU 核).

Fig.6 A flowchart of GPU accelerated SCF calculation
图 6 GPU 加速 SCF 计算流程图
后自洽场(post-SCF)计算在提高量子化学计算结果精度和研究前沿科学问题上有着非常重要的作用.作为
多参考方法起点的多组态(multi-configurational)自洽场的计算热点非常类似 Hartree-Fock 的计算,区别之处是
在多组态自洽场使用的积分常为分子轨道下的积分,自洽迭代过程中积分的多个指标需要进行持续的变换操
作.此部分计算同样兼具访存密集型和计算密集型的特点.基于多行列式的微扰计算则是成功地实现了 GPU 加
速,极具代表性的有 NWchem 软件中的 CCSD(T)方法.该法中的 CCSD 计算复杂,由 CPU 处理;后续基于 CCSD
波函数的微扰计算(即 T 部分)则交由计算能力较强的 GPU 来实现,需针对偶合簇波函数中的每一个行列式表
示的系数进行微扰校正,计算热点为密度矩阵同电子积分的乘积运算.
1.6 格点量子色动力学
量子色动力学(即 QCD)是一种强相互作用的规范理论,它和电弱统一理论(EW)通称为标准模型,是高能物
理研究的基本理论体系.QCD 描述了组成强作用粒子(强子)的夸克和与色量子数相联系的规范场的相互作用,
可统一地描述强子的结构和它们之间的强相互作用,被认为是有希望的强作用基本理论.格点量子色动力学(格
点 QCD)是从第一性原理出发的研究 QCD 的非微扰方法 [31] ,对于高能物理中的重大物理问题,如夸克禁闭、宇
宙早期演化、标准模型精确检验及超出标准模型新物理需寻找等研究有不可替代的作用.格点 QCD 方法的计
算模拟过程对高性能计算资源需求巨大,其计算过程体现出计算密集型特征,而其数据分析则体现出数据密集
型特征.计算精度和数据分析效率直接反映了格点 QCD 计算方法的应用水平.大规模计算应用中通常采用空间