Page 43 - 《软件学报》2021年第6期

郝宗寅 等:Petri 网的反向展开及其在程序数据竞争检测的应用 1617

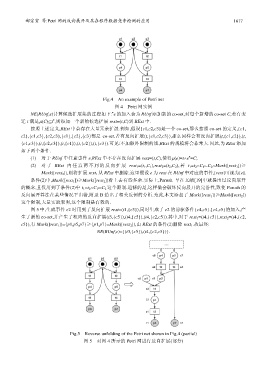
Fig.4 An example of Petri net
图 4 Petri 网实例
•
NE(RUnf,e)计算候选扩展集的过程如下: e 的加入会为 RUnf 添加新的 co-set,对每个新增的 co-set C,若有变
•
迁 t 满足μ(C)⊆t ,则添加一个新的候选扩展 rext=(t,C)到 RExt 中.
按照上述定义,RExt 中会存在大量冗余扩展.例如,假设{c1,c2,c3}是一个 co-set,那么按照 co-set 的定义,{c1,
c2},{c1,c3},{c2,c3},{c1},{c2},{c3}都是 co-set.若有反向扩展(t,{c1,c2,c3}),那么同样会有反向扩展(t,{c1,c2}),(t,
{c1,c3}),(t,{c2,c3}),(t,{c1}),(t,{c2}),(t,{c3}).可见:不加额外限制的话,RExt 的规模将会非常大.因此,为 RExt 添加
如下两个条件.
•
(1) 对于 RUnf 中任意事件 e,RExt 中不存在反向扩展 rext=(t,C),使得μ(e)=t∧e =C;
(2) 对于 RExt 内 任意两不同 的反向扩展 rext 1 =(t 1 ,C 1 ),rext 2 =(t 2 ,C 2 ), 若 t 1 =t 2 ∧C 1 ⊂C 2 ∧Mark([rext 1 ])≥
Mark([rext 2 ]),则将扩展 rext 1 从 RExt 中删除.这里假设 e 为 rext 在 RUnf 中对应的事件,[rext]可视为[e].
条件(2)中,Mark([rext 1 ])≥Mark([rext 2 ])看上去有些多余.实际上,Parosh 早在文献[19]中就提出过反向展开
的概念,且仅用到了条件(2)中 t 1 =t 2 ∧C 1 ⊂C 2 这个限制.遗憾的是,这样做会破坏反向展开的完备性,致使 Parosh 的
反向展开算法在某些情况下出错,附录 B 给出了相关反例的分析.为此,本文添加了 Mark([rext 1 ])≥Mark([rext 2 ])
这个限制,大量实践表明,这个限制是有效的.
图 5 中,生成事件 e2 时用到了反向扩展 rext=(t1,{c3}),同时生成了 e2 的前驱条件{c4,c5}.{c4,c5}的加入,产
生了新的 co-set,并产生了相应的反向扩展(t3,{c5}),(t4,{c5}),(t4,{c2,c5}).其中,对于 rext 1 =(t4,{c5}),rext 2 =(t4,{c2,
c5}),有 Mark([rext 1 ])={p1,p5,p7}≥{p1,p7}=Mark([rext 2 ]),由 RExt 的条件(2)删除 rext 1 .故最终:
NE(RUnf,e)={(t3,{c5}),(t4,{c2,c5})}.

Fig.5 Reverse unfolding of the Petri net shown in Fig.4 (partial)
图 5 对图 4 所示的 Petri 网进行反向扩展(部分)