Page 321 - 《软件学报》2021年第6期

麻莹莹 等:基于 Coq 的分块矩阵运算的形式化 1895

match l1,l2 with
|hd1::tl1,hd2::tl2⇒hd1===hd2∧list_Meq tl1 tl2
|nil,nil⇒True
|_,_⇒False
end.

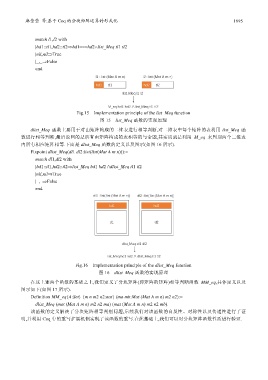
Fig.15 Implementation principle of the list_Meq function
图 15 list_Meq 函数的实现原理

dlist_Meq 函数主要用于对由矩阵构成的二维表进行相等判断,对二维表中每个矩阵的表利用 list_Meq 函
数进行相等判断,最后返回的是所有由矩阵构成的表相等的与命题,其实质就是利用 M_eq 来判别两个二维表
内所有相应矩阵相等.下面是 dlist_Meq 函数的定义以及图示(如图 16 所示).
Fixpoint dlist_Meq(dl1 dl2:list(list(Mat A m n))):=
match dl1,dl2 with
|hd1::tl1,hd2::tl2⇒list_Meq hd1 hd2 /\dlist_Meq tl1 tl2
|nil,nil⇒True
|_,_⇒False
end.

Fig.16 Implementation principle of the dlist_Meq function
图 16 dlist_Meq 函数的实现原理

在这上述两个函数的基础之上,我们定义了分块矩阵(即矩阵的矩阵)相等判断函数 MM_eq,具体定义以及
图示如下(如图 17 所示).
Definition MM_eq{A:Set} {m n m2 n2:nat} (ma mb:Mat (Mat A m n) m2 n2):=
dlist_Meq (mat (Mat A m n) m2 n2 ma) (mat (Mat A m n) m2 n2 mb).
该函数的定义解决了分块矩阵相等判别问题,后续我们对该函数的自反性、对称性以及传递性进行了证
明,并利用 Coq 中的重写扩展机制实现了该函数的重写.在此基础上,我们可以对分块矩阵函数性质进行验证.