Page 219 - 《软件学报》2021年第6期

陈小颖 等:面向 CPS 时空性质验证的混成 AADL 建模与模型转换方法 1793

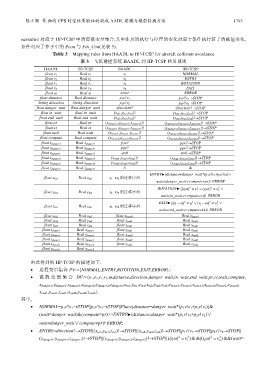
variables 对应于 HP-TCSP 中的离散变量集合,其中涉及的执行与位置的变化对应于条件执行算子的赋值变化,
条件对应于算子中的 Pcon 与 Fin_Con(见表 3).
Table 3 Mapping rules from HAADL to HP-TCSP for aircraft collision avoidance
表 3 飞机避撞系统 HAADL 到 HP-TCSP 映射规则
HAADL HP-TCSP HAADL HP-TCSP
float v 1 Real v 1 s 1 NORMAL
float v 2 Real v 2 s 2 ENTRY
float r 1 Real r 1 s 3 ROTATION
float r 2 Real r 2 s 4 EXIT
float ω Real ω error ERROR
float distance Real distance p 1v?v 1 p 1v?v 1→STOP
String direction String direction p 2v?v 2 p 2v?v 2→STOP
float danger_wait Real danger_wait direction? direction?→STOP
float in_wait Real in_wait (x in1,y in1,z in1)! (x in1,y in1,z in1)!→STOP
float end_wait Real end_wait (x in2,y in2,z in2)! (x in2,y in2,z in2)!→STOP
float pr Real pr (x danger2,y danger2,z danger2)! (x danger2,y danger2,z danger2)!→STOP
float ct Real ct (x danger1,y danger1,z danger1)! (x danger1,y danger1,z danger1)!→STOP
float wait Real wait (x leave1,y leave1,z leave1)! (x leave1,y leave1,z leave1)!→STOP
float compute Real compute (x leave2,y leave2,z leave2)! (x leave2,y leave2,z leave2)!→STOP
float x danger1 Real x danger1 p 1w? p 1w?→STOP
float y danger1 Real y danger1 p 2w? p 2w?→STOP
float z danger1 Real z danger1 ω=0 ω=0→STOP
float x danger2 Real x danger2 (x end1,y end1,z end1)! (x end1,y end1,z end1)!→STOP
float y danger2 Real y danger2 (x end2,y end2,z end2)! (x end2,y end2,z end2)!→STOP
float z danger2 Real z danger2 ∧ &
ENTRY (distance≠danger_wait*(p 1v!v 1+p 2v!v 2)∨
float x in1 Real x in1 s 1→s 2 的迁移序列
wait≠danger_wait∨compute≠pr)AERROR
ROTATION ((r 1 )ω 2 ≠ v 1 ∨ 2 2 ( ω ) ≠ r 2 2 2 v ∨
float y in1 Real y in1 s 2→s 3 的迁移序列
wait≠in_wait∨compute≠ct)AERROR
2
EXIT (( −r 1 ω ) ≠ 2 1 ∨ v 2 2 ( − r ω ) ≠ 2 2 v ∨
float z in1 Real z in1 s 3→s 4 的迁移序列
wait≠end_wait∨compute≠bk)AERROR
float x in2 Real x in2 float z leave2 Real z leave2
float y in2 Real y in2 float x end1 Real x end1
float z in2 Real z in2 float y end1 Real y end1
float x leave1 Real x leave1 float z end1 Real z end1
float y leave1 Real y leave1 float x end2 Real x end2
float z leave1 Real z leave1 float y end2 Real y end2
float x leave2 Real x leave2 float z end2 Real z end2
float y leave2 Real y leave2

由此得到的 HP-TCSP 的描述如下.
• 进程变量集合 PV:={NORMAL,ENTRY,ROTATION,EXIT,ERROR};
• 离散变量集 合 DV:={v 1 ,v 2 ,r 1 ,r 2 ,ω,distance,direction,danger_wait,in_wait,end_wait,pr,ct,wait,compute,
x danger1 ,y danger1 ,z danger1 ,x danger2 ,y danger2 ,z danger2 ,x in1 ,y in1 ,z in1 ,x in2 ,y in2 ,z in2 ,x leave1 ,y leave1 ,z leave1 ,x leave2 ,y leave2 ,z leave2 ,
x end1 ,y end1 ,z end1 ,x end2 ,y end2 ,z end2 }.
其中,
• NORMAL=p 1 v?v 1 →STOP||p 2 v?v 2 →STOP||Place[distance=danger_wait*(p 1 v!v 1 +p 2 v!v 2 )]&
(wait=danger_wait)&(compute=pr)>>ENTRY (distance≠danger_wait*(p 1 v!v 1 +p 2 v!v 2 )∨
wait≠danger_wait∨compute≠pr)AERROR;
• ENTRY=direction?→STOP||(x in1 ,y in1 ,z in1 )!→STOP||(x in2 ,y in2 ,z in2 )!→STOP||p 1 v?v 1 →STOP||p 2 v?v 2 →STOP||
(x danger1 ,y danger1 ,z danger1 )!→STOP||(x danger2 ,y danger2 ,z danger2 )!→STOP|| ((rω 1 ) = 2 v 1 2 ) & &((r ω 2 ) = 2 v 2 2 ) &&(wait=