Page 15 - 《软件学报》2021年第5期

殷康璘 等:基于混沌工程的微服务韧性风险识别和分析 1239

续值,为了判断连续数据的条件独立性 [74] ,本文使用了如下方法.
建立零假设 H 0 :性能指标 X,Y 在给定条件 C 下的偏相关系数ρ XY,C =0.其对应的备择假设 H 1 为:X,Y 在给定条
件 C 下的偏相关系数ρ XY,C ≠0.通过 F 检验验证 H 0 是否成立:若 H 0 成立,则说明监控指标 X,Y 在给定条件 C 下条
件独立,其实际意义为 X,Y 之间没有因果关系或者 X,Y 经由 C 产生了间接的因果关系.零假设 H 0 在 F 检验下的
显著性水平 z(ρ XY,C )的计算公式如公式(1)所示.
n− | C | 3− 1 ρ+
,
( z ρ XY ,C ) = ⋅ log XYC (1)
−
2 1 ρ XYC
,
其中,n 为混沌实验数据集中性能指标的数量,|C|为 C 中性能指标的数量.通过文献[75]中的论证可知,满足标准
正态分布.给定阈值 p(本文中 p=0.05),若|z|<p,则接受假设ρ XY,C =0,说明 X,Y 在给定条件 C 下独立,并删除因果关
系图中对应的边 X—Y.
3.3 因果关系边权重赋值
在第 3.2 节得到的性能指标之间的因果关系图中,一个性能指标会存在多条指向该指标的因果关系链路.
为了能够将多条因果关系链路排序,优先输出可能性较高的因果关系链路,本阶段为因果关系图中的每一条因
果关系边赋予权重值,作为因果关系链路的排序依据.由于韧性风险是基于微服务系统的服务降级上所提出的,
且服务性能指标的上升和下降通常由其他系统性能指标的上升和下降引起,本文将混沌实验数据集中各性能
指标的上升和下降变化作为因果关系边权重赋予的依据.如果在相近的时间段内两个性能指标同时发生了明
显的变化,则说明这两个性能指标很有可能是互相影响的.
借鉴文献[76]中判断一个事件是否对时序数据产生影响的思路,为了检测某一性能指标的上升和下降,本
文提出的分析方法将该项性能指标的时间序列数据按照指定的数据量依次划分成若干个数据窗口,对每两个
相邻的窗口Γ front ,通过 t 检验(student t’s test) 计算Γ front 和Γ rear 之间的检验统计量 t score .t score 的计算公式如公式
(2)所示.
μ front − μ
t = Γ Γ rear (2)
score 2 2
σ front + σ
Γ Γ rear
n − 1
其中,n 为数据窗口的大小, μ ,μ ,σ 2 ,σ 2 rear 分别为窗口Γ front 和Γ rear 内性能数据的均值和方差.若计算得
Γ front Γ rear Γ front Γ
到某两个窗口的 t score 的绝对值大于某个特定阈值在自由度 n−1 时对应的检验统计量(如在阈值为 0.05、窗口
大小为 20 时,t 检验对应的检验统计量为 1.7291),则说明性能指标在两个窗口之间性能发生了显著的上升或下
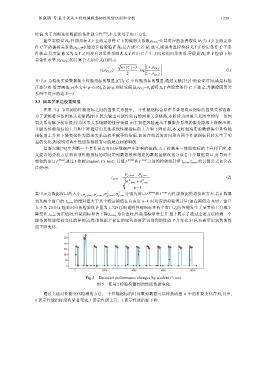
降变化.t score 为正值时,性能指标显著下降;t score 为负值时,性能指标显著上升.图 5 展示了通过上述方法检测一个
服务的性能指标变化的样例,在性能数据上标注的绿色点表示识别到的性能上升变化,红色点表示识别到的性
能下降变化.

Fig.5 Detected performance changes by student t’s test
图 5 使用 t 检验检测到的性能数据变化

通过上述对性能变化检测的方法,一个性能指标的时间数列数据可以转换成图 6 中的性能变化序列,其中,
0 表示性能指标没有显著变化,1 表示性能上升,−1 表示性能指标下降.