Page 347 - 《软件学报》2020年第11期

3662 Journal of Software 软件学报 Vol.31, No.11, November 2020

保持在关键级 1 下执行,那么 J 2 最晚将在时刻 3 之前获得 2 的执行时间并完成.当 J 2 发生过载,其执行时间增加
到 4, ddbf 2 1 ()t 在时刻 3 之后增加到 5.但依然能在它的时限时刻 5 满足: ddbf 2 1 (5) 5= ,也就是说,即使 J 2 发生了过
载,它也能在其时限 5 之前获得足够的执行时间,依然是可调度的.

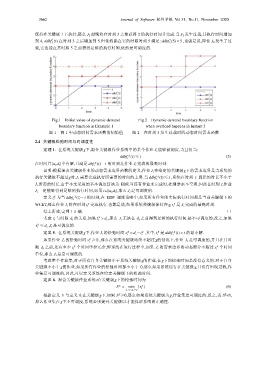
Fig.1 Initial value of dynamic demand Fig.2 Dynamic demand boundary function
boundary function in Example 1 when overload happens in Instant 3
图 1 例 1 中动态时间需求函数的初始值 图 2 在时刻 3 发生过载时的动态时间需求函数

2.4 关键级松弛时间与可调度性
定理 1. 在系统关键级χ下,混合关键级作业系统中的某个作业 J i 能够被调度,当且仅当:
ddbf χ () t ≤ t (5)
i
在时间片[a i ,d i ]中有解,且满足 dbf χ ()t = 的时刻是作业 J i 完成的最晚时刻.
t
i
证明:根据混合关键级作业的动态需求边界函数的定义,作业 J i 在给定的关键级χ下的需求边界是当系统的
执行关键级不超过χ时,J i 需要完成执行所需要的时间的上界.当 ddbf i χ ()t ≤ ,系统在时刻 t 提供的时长不小于
t
J i 所需的时长.由于本文采用的基本调度算法为 EDF,当还有作业未完成时,处理器永不空闲,因此在时刻 t,作业
J i 一定能够得到足够的执行时间,如果 t∈[a i ,d i ],那么 J i 是可调度的.
χ
t
定义 t 为当 ddbf i χ ()t = 的时刻,在 EDF 调度策略中,如果所有作业的实际执行时间都是当前关键级下的
i
χ
χ
WCET,那么作业 J i 将在时刻 t 完成执行.也就是说,如果系统关键级保持在χ, t 是 J i 完成的最晚时刻.
i
i
综上所述,定理 1 正确. □
考虑 t i 与时限 d i 的关系,如果 t > d ,那么 J i 无法在 d i 之前得到足够的执行时间,是不可调度的;反之,如果
χ
i i
χ
t ≤ d ,J i 是可调度的.
i i
χ
χ
定义 5. 在系统关键级χ下,作业 J i 的松弛时间 s = d − t ,其中, t 是 ddbf χ () t = 的最小解.
χ
t
i i i i i
χ
0
如果作业 J i 的松弛时间 s ≥ ,那么在系统关键级始终不超过χ的情况下,作业 J i 是可调度的,并且在其时
i
χ
χ
限 d i 之前,还有至少 s 个时间单位冗余.即系统在运行过程中,如果 J i 的需求边界的动态部分不超过 s 个时间
i i
单位,那么 J i 总是可调度的.
考虑整个作业集,对于所有自身关键级小于系统关键级χ的作业,在χ下的松弛时间是没有意义的.对于自身
关键级不小于χ的作业,如果所有作业的松弛时间都不小于 0,那么如果系统运行在关键级χ,且没有出现过载,作
业集是可调度的.因此,可以定义系统在给定关键级下的松弛时间.
定义 6. 混合关键级作业系统τ在关键级χ下的松弛时间为
χ
S = min { }s i χ (6)
∈
i J τχ χ
: i ≥
χ
χ
根据定义 3 与定义 6,在关键级χ下,如果 S ≥0,那么如果系统关键级为χ,作业集是可调度的;反之,当 S <0,
那么作业集在χ下不可调度,系统必须提升关键级以才能保证系统的正确性.