Page 124 - 《软件学报》2020年第11期

3440 Journal of Software 软件学报 Vol.31, No.11, November 2020

对于图 G,其所有的子图集表示为 sgG = () ∪ TreeWalk ( , , ),v G d ∀ i v ∈ i , G d ∈ {0,1,..., }D ,对于恶意程序数据流
图集{G 1 ,G 2 ,…,G n }中提取每个图的子图集 sg(G i )构造恶意程序的子图语料库 sg cors = sg (),G i = ∪ i 1,2,...,n ,子图
语料库包含了训练样本中恶意程序所有可能的恶意行为特征.

A
A

B C B C

D A D D

(a) (b)
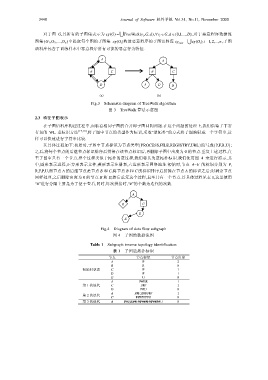
Fig.3 Schematic diagram of TreeWalk algorithm
图 3 TreeWalk 算法示意图
2.3 特征子图表示
在子图语料库构建过程中,面临着相同子图的合并即子图同构问题.在这个问题的处理上,我们借鉴了非常
有名的 WL 重标识方法 [17,18] ,将子图中节点的类型作为标识,采取“逆拓扑”的方式将子图映射成一个字符串,这
样可以快速进行字符串比较.
其具体过程如下:初始时,子图中节点标识为节点类型{PROCESS,FILE,REGISTRY,URL}简写成{P,F,R,U};
之后,将每个节点的后继节点标识排序后拼接在该节点标识后,再删除子图中出度为 0 的节点.重复上述过程,直
至子图中只有一个节点.整个过程类似于拓扑的逆过程,我们称其为逆拓扑标识.我们使用图 4 来进行演示,其
中,圆形表示进程,正方形表示文件,菱形表示注册表,六边形表示网络地址.初始时,节点 A~E 的标识分别为 P,
R,F,P,U,而节点 A 的后继节点是节点 B 和 C,将节点 B 和 C 的标识排序后拼接在节点 A 的标识之后;对剩余节点
同样处理,之后删除出度为 0 的节点 B 和 E;然后重复这个过程,直至只有一个节点.其具体过程见表 1,这里使用
“#”进行分隔主要是为了便于查看,同时,每次拼接时,“#”的个数为迭代的次数.

A

B C

D

E

Fig.4 Diagram of data flow subgraph
图 4 子图的数据流图

Table 1 Subgraph inverse topology identification
表 1 子图逆拓扑标识
节点 节点标识 节点出度
A P 2
B R 0
初始时状态 C F 1
D P 1
E U 0
A P#F,R 1
第 1 次迭代 C F#P 1
D P#U 0
A P#F,R##F#P 1
第 2 次迭代
C F#P##P#U 0
第 3 次迭代 A P#F,R##F#P###F#P##P#U 0