Page 168 - 《软件学报》2020年第12期

3834 Journal of Software 软件学报 Vol.31, No.12, December 2020

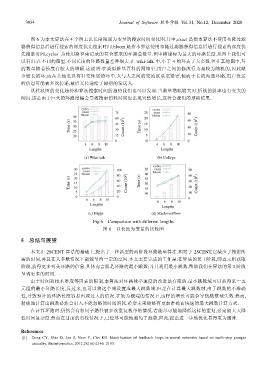
图 6 为本文算法在 4 个图上以长度限制为变量的搜索时间变化图,其中,exact 是指本算法不使用布隆过滤
器获得信息后进行搜索的深度优先搜索时间,bloom 是指本算法使用布隆过滤器获得信息后进行搜素的深度优
先搜索时间,cycles 为使用路径束记录的符合要求的环路总数量.图中横坐标为最大的环路长度.从图上我们可
以看出:在不同的图里,不同长度的环路数量差异很大.在 wiki-talk 中,小于 4 的环占了大多数.但在其他图中,环
的数量随着长度有较大的增幅.这说明:在类似维基百科的网络中,用户之间的修改行为是较为随机的,因此缺
少较长的环;而在其他更具有社交性质的环中,人与人之间的交流联系更紧密,倾向于长的沟通环路,用户发送
的信息可能被多次传递,最后又传递给了最初的发送人.
从柱状图的变化趋势和算法搜索时间的趋势我们也可以发现:当数量增幅较大时,折线的斜率也有变大的
倾向.这是由于巨大的环路增幅会导致搜索消耗时间也出现突然增长,这符合我们的预期结果.

Time (s) Count (10 3 ) Time (s) Count (10 3 )

(a) Wiki-talk (b) College

Time (s) Count (10 3 ) Time (s) Count (10 3 )

(c) Higgs (d) Stackoverflow
Fig.6 Comparison with different lengths
图 6 以长度为变量的比较图

5 总结与展望
本文在 2SCENT 算法的基础上,提出了一种新型的两阶段环路枚举算法.相对于 2SCENT,它减少了搜索所
需的时间,并且在大多数情况下都能节约一定的空间.本文主要完成的工作是:在算法的第 1 阶段,即五元组获取
阶段,获得更多有关环路的信息,具体而言就是环路的最小跳数;并且利用最小跳数,帮助我们在算法的第 2 阶段
节省更多的时间.
由于时间和技术难度等因素的限制,本算法对环路枚举速度的改进是有限的.最小跳数域可以获得某一五
元组的最小环路长度,反过来,也可以将这个域设置成最大跳数域.但是在计算最大跳数时,由于跳数的不准确
性,导致预计的环路长度容易出现过大的情况.在较为极端的情况下,这样的增长可能会导致跳数域失效.然而,
精确地计算出跳数必然会引入不能忽略的时间消耗.希望未来能够有更加准确而快速的最大跳数计算方式.
在计算环路时,仍然会有相同子路径被多次重复枚举的情况.若能尽可能地降低这样的重复,必定能大大降
低时间复杂度.然而在目前的剪枝情况下,已经尽可能地避免了浪费,因此,提出进一步地优化显得更为困难.

References:
[1] Dong CY, Shin D, Joo S, Nam Y, Cho KH. Identification of feedback loops in neural networks based on multi-step granger
causality. Bioinformatics, 2012,28(16):2146−2153.